狄拉克δ函数(Dirac delta)

在卷积那篇文章中，已经提到了狄拉克δ函数的定义:

\[ delta (t) = \begin {cases} +\infty , t=0 \\ 0, t\neq 0 \end {cases} \]

\[ \int _{-\infty }^{\infty }\delta (t)dt = 1 \]

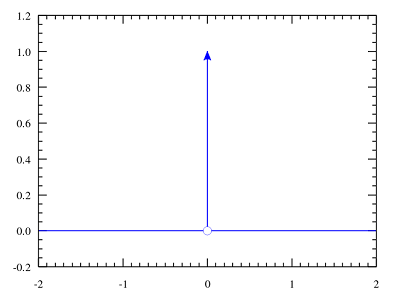
下面介绍它的一些性质:

对称性质

从δ函数的波形图(或者定义)可以简单看出，δ函数是偶函数，即:

\[ \delta (t) = \delta (-t) \]

缩放性质

设有常数a，令u = at，再依据δ函数的积分特性，有:

\[ dt = \frac {1}{a}du \]

\[ \int _{-\infty }^{\infty }\delta (at)dt = \int _{-\infty }^{\infty }\delta (u)\frac {1}{a}du = \frac {1}{a} \int _{-\infty }^{\infty }\delta (u)du = \frac {1}{a} \]

也即:

\[ \delta (at) = \frac {1}{a}\delta (t) \]

又因为它的对称性质，有:

\[ \delta (at) = \frac {1}{|a|}\delta (t) \]

代数性质

\[ t\delta (t) = 0 \]

这个太简单了，从基本定义出发可以很快看出来这个式子的正确性。

平移性质

\[ \int _{-\infty }^{\infty }f(t)\delta (t - T)dt = f(T) \]

在理解卷积 Convolution中有对这个式子的详细讨论。当然从δ函数的定义去理解这个式子也很简单。

δ函数的傅里叶变换

\[ \mathcal {F}[\delta (s)] = \int _{-\infty }^{\infty }e^{-2\pi ist}\delta (t) = 1 \]

因为只有当x等于0时，δ函数才非0(等于1)，所以这个式子的计算结果等于1。

傅里叶变换后是一个常数1，这个性质看起来就很特别。

狄拉克梳状函数(Dirac comb)

这个函数在电子工程electrical engineering中称为脉冲序列(impulse train)或采样函数(sampling function)。注意，有些文章会把它叫做Shah function。

它其实就是关于狄拉克δ函数的用周期T间隔的无穷级数(多个δ函数的合并)。(wiki原文是:A Dirac comb is an infinite series of Dirac delta functions spaced at intervals of T）

用图表示:

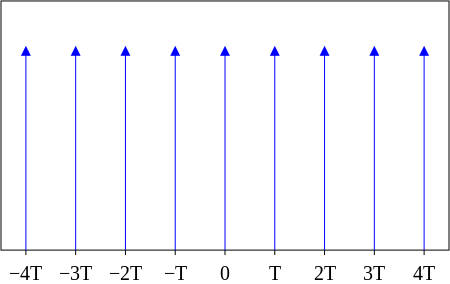
(图片来自wiki）

公式表示:

\[ III_{T}(t) = \sum _{k=-\infty }^{\infty }\delta (t - kT)\]

这个公式和图片完全对应。

下面介绍它的一些性质:

缩放性质

当T = 1（单位周期）时：

\[ III(t) = \sum _{k=-\infty }^{\infty }\delta (t - k)\]

这时再对t缩放a倍:

\[ III(at) = \sum _{k=-\infty }^{\infty }\delta (at - k)\]

现在搬出δ函数的对称性质公式:

\[ \delta (at) = \frac {1}{a}\delta (t) \]

\[ III(at) = \sum _{k=-\infty }^{\infty }\delta (at - k) \] \[ = \sum _{k=-\infty }^{\infty }\delta (a(t - \frac {k}{a})) \] \[ = \sum _{k=-\infty }^{\infty }\frac {1}{a}\delta (t - \frac {k}{a}) \]

\[ = \frac {1}{a}III_{\frac {1}{a}}(t)\]

也就是:

\[ III(at) = \frac {1}{a}III_{\frac {1}{a}}(t) \]

\[ III_{a}(t) = \frac {1}{a}III_{}(\frac {t}{a}) \]

傅里叶变换

\[ III_{a}(t) = \frac {1}{T}\sum _{k=-\infty }^{\infty }e^{2\pi is\frac {t}{T}} \]

(未经授权禁止转载)