三种坐标系

矩坐标

矩坐标似乎是中文网络上才有的说法，正确叫法是笛卡尔坐标系。

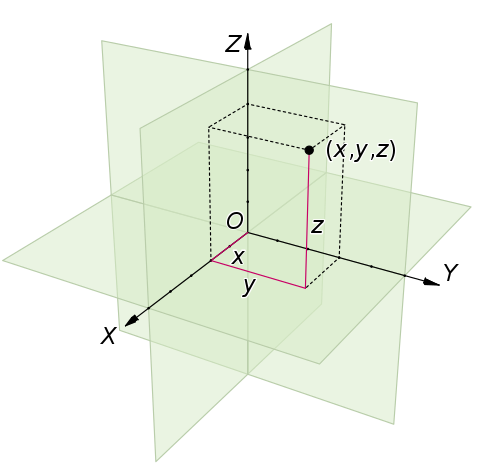
柱坐标

柱坐标其实就是圆的定义的延伸。柱的横截面是圆，圆有一个半径r和角度φ，柱则还有一个厚度维度z。

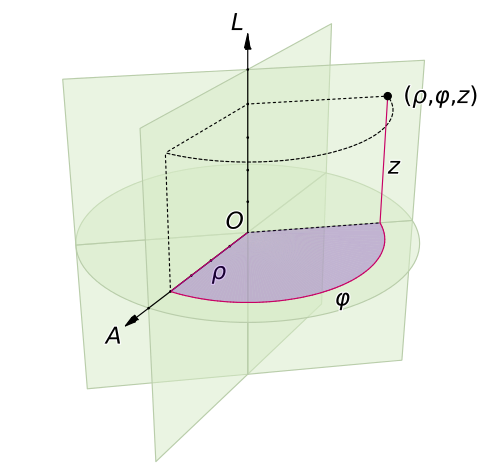
球坐标

球坐标是极坐标的三维形式。

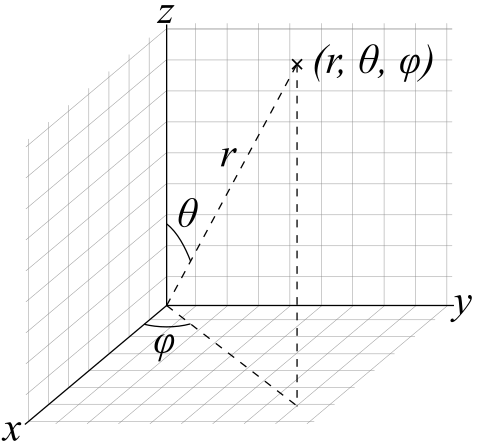
基函数和投影和重建

基函数和正交

假设3D空间中有一个点P，记它的位置为函数f，f究竟是个什么东西呢？或者说怎么用数学描述f？

答案是用坐标系，坐标系的本质就是一组正交的基函数(basis)。

大家知道3D空间的笛卡尔坐标系有3个basis：(1,0,0)、(0,1,0)、(0,0,1)。这3个基向量是正交的。

正交性有2个特点：

• 任意2个不同的basis之间点积结果为0
• 任意一个basis和它自己做点积，结果为常数c

用积分式子表达这个正交关系：

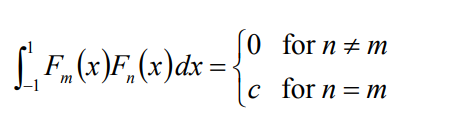
（当C为1时，其中的F称为正交基函数orthonormal basis functions）

有了这个概念后，f这个事情就有了下一步的方向了：怎么用(1,0,0)、(0,1,0)、(0,0,1)描述f？

投影

假设这个3D空间中有另一个参数物O，那么P究竟离O*有多远呢*

假设没有其他工具、且人眼变成了一个正交相机，那么可以用三视角来判断P和O的距离：

• 站在P的正面，观察P和O的相对位置，即得到P在xy平面的投影点
• 站在P的侧面，观察P和O的相对位置，即得到P在yz平面的投影点
• 站在P的头顶，观察P和O的相对位置，即得到P在xz平面的投影点

平面上的投影点P'，和O的关系又怎么办呢？因为我们已经通过三视图把三维问题降成了二维问题，同理也可以把二维问题降到一维，即继续把P投影到三个basis轴上得到P''。P''和O的距离就好办了，用尺子量。

通过这个降维的办法，最终就能得到P在三个basis(1,0,0)、(0,1,0)、(0,0,1)上的投影距离x、y、z，一般也叫投影系数。也可记为：(x,0,0)、(0,y,0)、(0,0,z）。投影系数数量等于basis数量。

同时f可以记为f=(x,y,z)。f的投影过程可以数学描述了。

记basis为\(\mathbf B_{i}\), f在\(\mathbf B_{i}\)投影系数记为\(C_{i}\)，并拓展f到任意维度、任意坐标系：

\[ C_{i} = \mathbf f \cdot \mathbf B_{i} \]

验证：

\[ (x,y,z) \cdot (1,0,0) = x \] \[ (x,y,z) \cdot (0,1,0) = y \] \[ (x,y,z) \cdot (0,0,1) = z \]

到了这里，f到三个basis的投影问题就解决了。接下来讨论的是怎么用basis和投影参数，重建f。

重建

很简单，f其实就是三个basis和三个投影系数分别相乘后的累加：

\[ (1,0,0) * x = (x,0,0) \] \[ (0,1,0) * y = (x,y,0) \] \[ (0,0,1) * z = (0,0,z) \] \[ f = (1,0,0) * x + (0,1,0) * y + (0,0,1) * z = (x,y,z) \]

也可以用矩阵的形式表达：

\[ \mathbf f = \left[ \begin{matrix} 1&0&0\\ 0&1&0\\ 0&0&1\\ \end{matrix} \right] \left[ \begin{matrix} x\\ y\\ z\\ \end{matrix} \right] \]

更标准的描述：

\[ \mathbf f = \sum_{i=1}^{n} \mathbf B_{i} C_{i} \]

注意这里的\(\mathbf B_{i}\)基函数究竟是什么样的是不确定的，可能是上面的笛卡尔基函数，也可能是球坐标基函数，当然最重要的是下文会提到的球谐基函数。

综上，当f未知而\(C_{i}\)已知时，我们可以用上述公式重建出f。

数学期望和蒙特卡洛积分

数学期望

数学期望是随机变量输出值的加权平均，连续随机变量的数学期望公式如下：

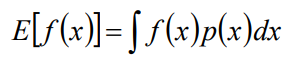
其中的p是概率密度函数，p的积分需要等于1。

举一个例子，求f(x) = 2 - x在定义域[0, 2]的数学期望值。需要先构造一个概率密度函数p，p显然等于1/2。于是有：

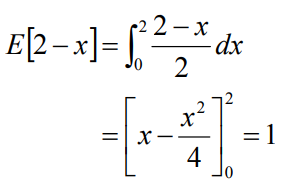
蒙特卡洛积分

对于没有解析式或者不好算积分的f(x)，可以用离散采样f(x)并加权求平均的方法求数学期望：

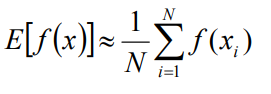
再结合上一节的式子：

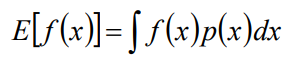
就可以用来算f(x)的积分了（不是数学期望！）：

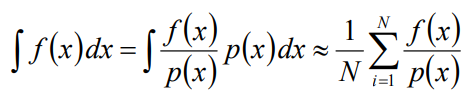
这也就是所谓的蒙特卡洛积分了。

(未经授权禁止转载)