很久前总结了pbr公式内容:PBR渲染原理,但没有说到各向异性的问题。
最近发现Filament详细介绍了pbr相关的知识,也有源码可读,可以好好学习一番。
pbr理论中,高光项的公式如下:
\[ f_ r(v,l) = \frac { D(h,\alpha ) G(v,l,\alpha ) F(v,h,F_0) } { 4 (n \cdot v)(n \cdot l) } \]
Filament用一个specularLobe统一描述了各向同性和各向异性的高光项:
vec3 specularLobe(const PixelParams pixel, const Light light, const vec3 h,
float NoV, float NoL, float NoH, float LoH) {
#if defined(MATERIAL_HAS_ANISOTROPY)
return anisotropicLobe(pixel, light, h, NoV, NoL, NoH, LoH);
#else
return isotropicLobe(pixel, light, h, NoV, NoL, NoH, LoH);
#endif
}
本文的目标是理解这里面的代码。
Filament的着色流程
代码都在shaders/src目录,根据宏变体,会组合这里面的代码,最终生成目标shader。
main.fs的main是入口:
void main() {
filament_lodBias = frameUniforms.lodBias;
// See shading_parameters.fs
// Computes global variables we need to evaluate material and lighting
computeShadingParams(); // 计算一些全局参数
// Initialize the inputs to sensible default values, see material_inputs.fs
MaterialInputs inputs;
initMaterial(inputs); // 初始化默认值
// Invoke user code
material(inputs); //调用.mat文件里的用户代码
fragColor = evaluateMaterial(inputs); // 着色
...
}
其中的evaluateMaterial具体是哪一个实现,得看选择的shading model。以基本的pbr为例(即LIT模型),代码在shading_lit.fs:
vec4 evaluateLights(const MaterialInputs material) {
PixelParams pixel;
getPixelParams(material, pixel); // 从材质参数转换得到后续计算用的PixelParams
vec3 color = vec3(0.0);
evaluateIBL(material, pixel, color); // 默认都有IBL间接光
#if defined(HAS_DIRECTIONAL_LIGHTING)
evaluateDirectionalLight(material, pixel, color); // 下面会分析的重点接口
#endif
...
return vec4(color, computeDiffuseAlpha(material.baseColor.a));
}
vec4 evaluateMaterial(const MaterialInputs material) {
vec4 color = evaluateLights(material);
addEmissive(material, color); // 自发光,先忽略
return color;
}
然后就看evaluateDirectionalLight,代码在light_directional.fs:
void evaluateDirectionalLight(const MaterialInputs material,
const PixelParams pixel, inout vec3 color) {
Light light = getDirectionalLight();
...
float visibility = 1.0;
#if defined(HAS_SHADOWING)
//算阴影 得到visibility
...
#endif
#if defined(MATERIAL_HAS_CUSTOM_SURFACE_SHADING)
color.rgb += customSurfaceShading(material, pixel, light, visibility);
#else
color.rgb += surfaceShading(pixel, light, visibility); // 重点
#endif
}
surfaceShading的代码在shading_model_standard.fs,这个就已经是pbr的核心代码了。
几个材质关键参数的计算
MaterialInputs是用户端的参数,即给美术编辑用的:
struct MaterialInputs {
vec4 baseColor;
float roughness;
float metallic;
float reflectance;
float ior;
...
}
PixelParams存了每个着色点的基本系数,一般这些系数和具体的着色算法无关:
struct PixelParams {
vec3 diffuseColor;
float perceptualRoughness;
float perceptualRoughnessUnclamped;
vec3 f0;
float roughness;
vec3 dfg;
vec3 energyCompensation;
...
}
根据MaterialInputs计算PixelParams的代码,主要是算了pixel.diffuseColor和pixel.f0 :
vec3 computeDiffuseColor(const vec4 baseColor, float metallic) {
return baseColor.rgb * (1.0 - metallic);
}
void getCommonPixelParams(const MaterialInputs material, inout PixelParams pixel) {
vec4 baseColor = material.baseColor;
pixel.diffuseColor = computeDiffuseColor(baseColor, material.metallic);
#if !defined(SHADING_MODEL_SUBSURFACE) && (!defined(MATERIAL_HAS_REFLECTANCE) && defined(MATERIAL_HAS_IOR))
float reflectance = iorToF0(max(1.0, material.ior), 1.0);
#else
// Assumes an interface from air to an IOR of 1.5 for dielectrics
float reflectance = computeDielectricF0(material.reflectance);
#endif
pixel.f0 = computeF0(baseColor, material.metallic, reflectance);
...
}
pixel.roughness和pixel.perceptualRoughness
原文解释 Roughness remapping and clamping
material.roughness被叫做用户设置的perceptualRoughness,pixel.roughness是真正用于pbr计算的Roughness。
\[pixel.roughness = material.roughness ^2 \]
直观理解就是,当美术设置了0.5的粗糙度时,实际的渲染是用的0.25。0.25渲染出来的效果,会让美术好理解。
如果直接让美术控制实际的粗糙度,那么当渲染比较光滑的物体时,粗糙度范围会小到很难设置,大约在[0, 0.05]之间。
代码:
float perceptualRoughnessToRoughness(float perceptualRoughness) {
return perceptualRoughness * perceptualRoughness;
}
void getRoughnessPixelParams(const MaterialInputs material, inout PixelParams pixel) {
float perceptualRoughness = material.roughness;
pixel.perceptualRoughnessUnclamped = perceptualRoughness;
pixel.perceptualRoughness = clamp(perceptualRoughness, MIN_PERCEPTUAL_ROUGHNESS, 1.0);
pixel.roughness = perceptualRoughnessToRoughness(pixel.perceptualRoughness);
}
pixel.diffuseColor
从computeDiffuseColor可见,metallic越大,pixel.diffuseColor就越接近黑色,黑色即表示几乎没有漫反射光。
pixel.f0
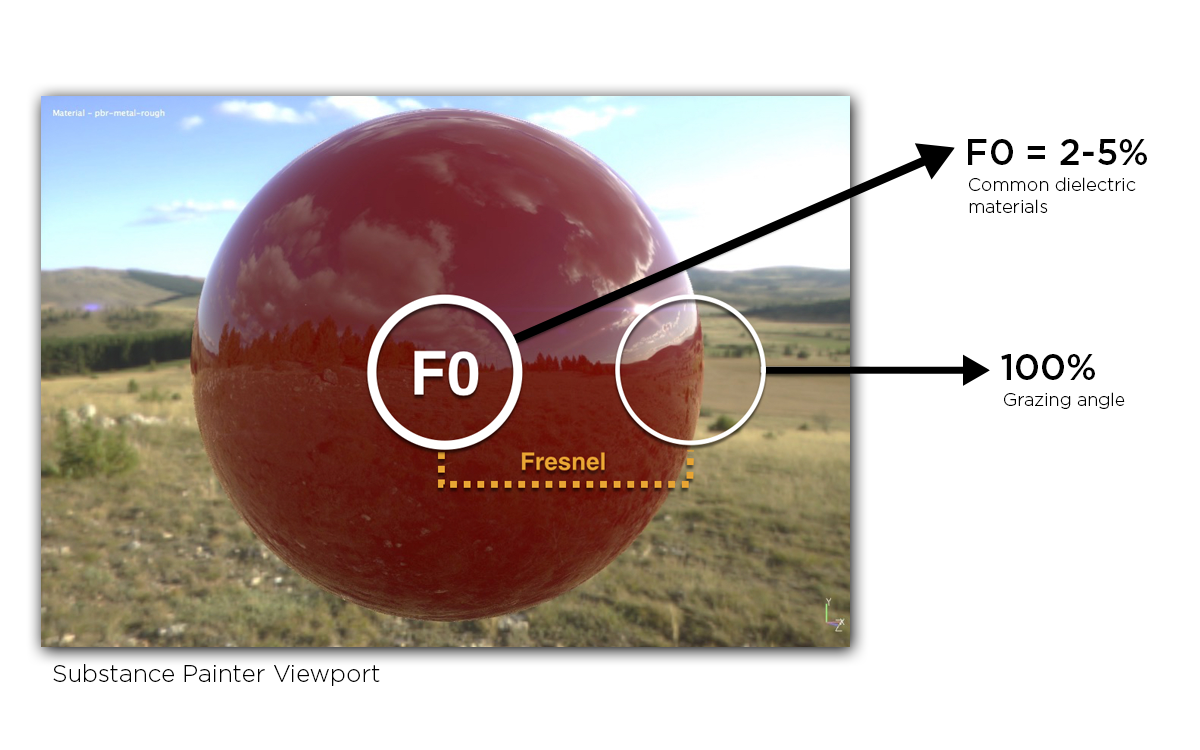
首先是理解什么是F0, F0等于 Fresnel Reflectance at 0 Degrees,是一个介于0到1的数,它表示当入射光线和表面垂直时,有x%的radiance变成镜面反射出去(剩下的1-x%发生折射)。
为什么要知道F0呢,因为pbr计算过程中有一个费涅尔项F(Fresnel term),需要用到F0。
有几个重要知识点要记一下:
- 电介质(dielectrics)的F0是非彩色的(achromatic),即认为RGB各分量相等
- 金属(metallic)的F0是彩色的(chromatic),RGB分量不相等
- F90必然等于1.0,F90表示当光线以grazing angles打到表面时,100%发生镜面反射,无论是电介质还是金属都一样
- 一般来说,大部分电介质的F0是4%;水是2%;F0最高的电介质是宝石(gemstones),16%左右。
F0计算方法1
为了方便美术调节F0,于是业界大佬发明了映射公式:
\[ f_0 = 0.16 \cdot f_{linear} ^2 \]
\(f_{linear}\)是个0到1的线性值,其中0.5对应水的F0(2%),1.0对应宝石的F0(16%)。Filament shader里的material.reflectance即是\(f_{linear}\),computeDielectricF0就是做这个映射的接口:
float computeDielectricF0(float reflectance) {
return 0.16 * reflectance * reflectance;
}
F0计算方法2
另一种算法是基于材质的ior。ior是指光穿过两种介质界面时的折射率,例如空气\(\rightarrow \)水界面的ior是1.33。
ior也是一个给美术调节的系数,即Filament shader里的material.ior。
ior涉及到两种介质,但在游戏里一般其中一种介质是空气,因此可以认为,各种介质相对空气的ior,即为该介质的ior,记为\(n_{ior}\)。空气的(n_{ior}\)即为1。
由ior算F0的公式如下:
\[ f_0 ( n_{ior} ) = ( \frac {n_{ior} - 1}{n_{ior} + 1} ) ^2 \]
这条公式不是随便拟合出的,是真实的物理公式简化得到的。详情可阅读:
涉及到极化性质什么的,就不细究了。
总之能简化成上述公式的原因是,\(f_{0}\)描述的是垂直角度的反射率。
另外补充一下,当其中一种介质并不是空气时,此时也可以根据这两种介质相对空气的ior,来算\(f_{0}\),公式如下:
\[ f_0 = ( \frac { n_{1} - n_{2} }{ n_{1} + n_{2} } ) ^2 \]
分子分母同时除以\(n_{2}\),就和前一条公式差不多了:
\[ f_0 = ( \frac { \frac {n_{1} } { n_{2} } - 1 }{ \frac {n_{1} } { n_{2} } + 1 } ) ^2 \]
当\(n_{2}\)为空气的ior 1.0时,就是第一条公式了。
Filament中的实现代码如下:
float iorToF0(float transmittedIor, float incidentIor) {
return sq((transmittedIor - incidentIor) / (transmittedIor + incidentIor));
}
transmittedIor即\(n_{1}\),incidentIor即\(n_{2}\)。
调用代码:
float reflectance = iorToF0(max(1.0, material.ior), 1.0);
可见,Filament直接约束了transmittedIor不低于1,且让incidentIor固定为空气ior 1.0。
根据material.metallic插值
上面算出来的\(f_{0}\)是个标量(scalar)(非彩色),只限定于电介质,为了和金属材质统一起来,所以还需要根据材质的metallic(金属度),做插值:
vec3 computeF0(const vec4 baseColor, float metallic, float reflectance) {
return baseColor.rgb * metallic + (reflectance * (1.0 - metallic));
}
pixel.f0 = computeF0(baseColor, material.metallic, reflectance);
可见,金属度越高,pixel.f0越接近于材质属性里的baseColor(彩色);金属度越低,越接近前面算出来的电介质reflectance(非彩色)。
isotropic specular
先从各向同性开始:
vec3 isotropicLobe(const PixelParams pixel, const Light light, const vec3 h,
float NoV, float NoL, float NoH, float LoH) {
float D = distribution(pixel.roughness, NoH, h);
float V = visibility(pixel.roughness, NoV, NoL);
vec3 F = fresnel(pixel.f0, LoH);
return (D * V) * F;
}
发现代码里少了\( 4 (n \cdot v)(n \cdot l) \)部分,这是因为Filament把specular公式拆成三部分:
\[ f_ r(v,l) = D(h,\alpha ) \cdot \frac { G(v,l,\alpha ) } { 4 (n \cdot v)(n \cdot l) } \cdot F(v,h,F_0) = D \cdot V \cdot F \]
\( 4 (n \cdot v)(n \cdot l) \)被放进了V项中了。
isotropic-D项
Filament里只有GGX一种(说明够用):
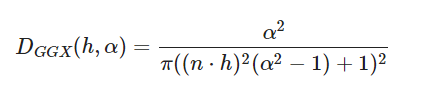
做一些变换,方便和代码对应:
\[ D = \frac {1}{\pi } \cdot (\frac {\alpha } { (n\cdot h)^ 2(\alpha ^ 2 - 1) + 1 })^ 2 \]
\[ = \frac {1}{\pi } (\frac {\alpha } { (n\cdot h)^ 2 \alpha ^ 2 - (n\cdot h)^ 2 + 1 })^ 2 \]
\[ = \frac {1}{\pi } (\frac {\alpha } { ( (n\cdot h) \alpha) ^ 2 + (1 - (n\cdot h)^ 2) })^ 2 \]
代码如下:
float D_GGX(float roughness, float NoH, const vec3 h) {
float oneMinusNoHSquared = 1.0 - NoH * NoH;
float a = NoH * roughness;
float k = roughness / (oneMinusNoHSquared + a * a);
float d = k * k * (1.0 / PI);
return saturateMediump(d);
}
float distribution(float roughness, float NoH, const vec3 h) {
#if BRDF_SPECULAR_D == SPECULAR_D_GGX
return D_GGX(roughness, NoH, h);
#endif
}
isotropic-G项
G项的话,Filament用了这篇论文里的equation 99: Understanding the Masking-Shadowing Function in Microfacet-Based BRDFs。这条公式的好处推导相当复杂,直接用即可。
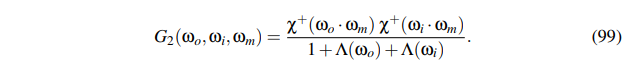
里面的符号的解释:
\(\omega _o\), \(\omega _i\), \(\omega _m\)分别表示出射方向、入射方向、微平面法线方向。
\(\chi ^+ \) 是指heaviside function,也叫unit step function,单位阶跃函数,值要么是0要么是1。
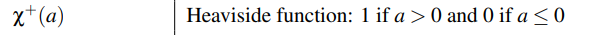
因为specular只考虑反射光,所以出入射方向和微平面法线夹角小于180°,分子等于1。
另外因为\( 4 (n \cdot v)(n \cdot l) \)被合并到了G项里(所以就换了个名字叫V项)。
最终的V公式如下:
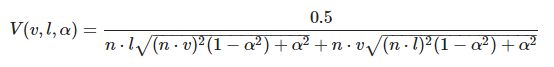
float V_SmithGGXCorrelated(float roughness, float NoV, float NoL) {
float a2 = roughness * roughness;
float lambdaV = NoL * sqrt((NoV - a2 * NoV) * NoV + a2);
float lambdaL = NoV * sqrt((NoL - a2 * NoL) * NoL + a2);
float v = 0.5 / (lambdaV + lambdaL);
return saturateMediump(v);
}
这里又有个经典技巧,牺牲精度换时间。因为开平方和平方操作都比较耗,直接干掉,公式变成:
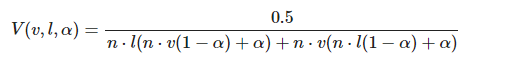
这个只是近似公式,数学上是错的,但不用深究,用就是了。
float V_SmithGGXCorrelated_Fast(float roughness, float NoV, float NoL) {
/*
float a = roughness;
float GGXV = NoL * (NoV * (1.0 - a) + a);
float GGXL = NoV * (NoL * (1.0 - a) + a);
return 0.5 / (GGXV + GGXL);
*/
float v = 0.5 / mix(2.0 * NoL * NoV, NoL + NoV, roughness);
return saturateMediump(v);
}
float visibility(float roughness, float NoV, float NoL) {
#if BRDF_SPECULAR_V == SPECULAR_V_SMITH_GGX
return V_SmithGGXCorrelated(roughness, NoV, NoL);
#elif BRDF_SPECULAR_V == SPECULAR_V_SMITH_GGX_FAST
return V_SmithGGXCorrelated_Fast(roughness, NoV, NoL);
#endif
}
isotropic-F项
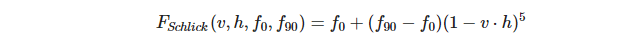
\(f_{0}\)、\(f_{90}\)上面已经分析过了,不再介绍。
当\(f_{90}\)为1时,有以下等价公式:
\[ f_{90} = 1\]
\[ f = (1 - v\cdot h)^ 5 \]
\[ F = f_{90}(1 - v\cdot h)^ 5 + f_{0}( 1 - (1 - v\cdot h)^ 5 ) \]
\[ = (1 - v\cdot h)^ 5 + f_{0}( 1 - (1 - v\cdot h)^ 5 ) \]
\[ = f + f_{0}( 1 - f ) \]
vec3 F_Schlick(const vec3 f0, float VoH) {
float f = pow(1.0 - VoH, 5.0);
return f + f0 * (1.0 - f);
}
float F_Schlick(float f0, float f90, float VoH) {
return f0 + (f90 - f0) * pow5(1.0 - VoH);
}
vec3 fresnel(const vec3 f0, float LoH) {
#if FILAMENT_QUALITY == FILAMENT_QUALITY_LOW
return F_Schlick(f0, LoH); // f90 = 1.0
#else
float f90 = saturate(dot(f0, vec3(50.0 * 0.33)));
return F_Schlick(f0, f90, LoH);
#endif
}
代码里实现了一种更准确的F项,具体细节看这里: Specular occlusion
anisotropic specular
各向异性的specular,也是基于pbr公式改的。
anisotropic-D项
首先是D项发生了变化:
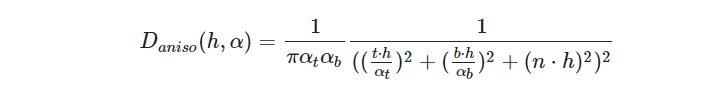
其中多了2个新的标量参数\( \alpha _{t}\)和\( \alpha _{b}\), 即\( \alpha _{tangent}\)和\( \alpha _{bitangent}\),切线方向的粗糙度和副切线方向的粗糙度。
以及多了2个向量t和b,即切线和副切线。
\( \alpha _{t}\)和\( \alpha _{b}\)的计算方法如下:
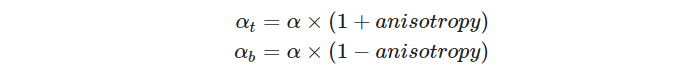
float at = max(pixel.roughness * (1.0 + pixel.anisotropy), MIN_ROUGHNESS);
float ab = max(pixel.roughness * (1.0 - pixel.anisotropy), MIN_ROUGHNESS);
切线pixel.anisotropicT和副切线pixel.anisotropicB是在世界空间下的,它们的计算代码如下:
void getAnisotropyPixelParams(const MaterialInputs material, inout PixelParams pixel) {
vec3 direction = material.anisotropyDirection;
pixel.anisotropy = material.anisotropy;
pixel.anisotropicT = normalize(shading_tangentToWorld * direction);
pixel.anisotropicB = normalize(cross(getWorldGeometricNormalVector(), pixel.anisotropicT));
}
切线空间下的切线方向direction,本来应该是从纹理读的,但性能考虑,直接用材质参数material.anisotropyDirection了。
再来看D项公式的化简:
\[ D_{aniso}(h,\alpha ) = \frac{1}{\pi \alpha _t \alpha _b} \frac{1}{ ((\frac {t\cdot h}{\alpha _t})^2 + (\frac {b\cdot h}{\alpha _b})^2 + (n\cdot h)^2)^2 } \]
令:
\[ d = (\frac {t\cdot h}{\alpha _t}, \frac {b\cdot h}{\alpha _b}, n\cdot h) \]
得到:
\[ D_{aniso}(h,\alpha ) = \frac{1}{\pi \alpha _t \alpha _b} \frac{1}{ (d\cdot d)^2 } \]
再设d':
\[ d' = \alpha _t \alpha _b d = (\alpha _b t\cdot h,\alpha _t b\cdot h, \alpha _t \alpha _b n\cdot h) \]
于是:
\[ d = \frac {d'}{\alpha _t \alpha _b} = \frac {(\alpha _b t\cdot h,\alpha _t b\cdot h, \alpha _t \alpha _b n\cdot h)}{\alpha _t \alpha _b} \]
\[ d\cdot d = \frac {d'\cdot d'}{(\alpha _t \alpha _b)^2} \]
\[ (d\cdot d)^2 =\frac { (d'\cdot d')^2 }{(\alpha _t \alpha _b)^4} \]
\[ \frac { 1 } { (d\cdot d)^2 } = \frac { (\alpha _t \alpha _b)^4 }{ (d'\cdot d')^2 } \]
\[ D_{aniso}(h,\alpha ) = \frac{1}{\pi \alpha _t \alpha _b} \frac { (\alpha _t \alpha _b)^4 }{ (d'\cdot d')^2 } = \frac{1}{\pi } \frac { (\alpha _t \alpha _b)^3 }{ (d'\cdot d')^2 } \]
完整的D项代码如下,和推导出来的公式对得上:
float D_GGX_Anisotropic(float at, float ab, float ToH, float BoH, float NoH) {
float a2 = at * ab;
highp vec3 d = vec3(ab * ToH, at * BoH, a2 * NoH);
highp float d2 = dot(d, d);
float b2 = a2 / d2;
return a2 * b2 * b2 * (1.0 / PI);
}
anisotropic-V项
各向异性的V项公式贼复杂,就不研究了,直接套代码即可。需要的参数上面都介绍过了:
float visibilityAnisotropic(float roughness, float at, float ab,
float ToV, float BoV, float ToL, float BoL, float NoV, float NoL) {
#if BRDF_ANISOTROPIC_V == SPECULAR_V_SMITH_GGX
return V_SmithGGXCorrelated(roughness, NoV, NoL);
#elif BRDF_ANISOTROPIC_V == SPECULAR_V_GGX_ANISOTROPIC
return V_SmithGGXCorrelated_Anisotropic(at, ab, ToV, BoV, ToL, BoL, NoV, NoL);
#endif
}
从代码里看出,可以直接用各向同性的V项。
anisotropic-F项
各向异性的F项和各向同性的F项一样。
写作不易,您的支持是我写作的动力!

