学习离线渲染最好从这99行代码开始：

smallpt: Global Illumination in 99 lines of C++

但这份代码有些小问题：

• 所有对象都是sphere。如果场景基于mesh的话，代码要改不少。
• 为了压缩行数，一些代码的理解不太直观。

进阶一点的话看：

Ray Tracing in One Weekend

为什么叫路径追踪Path tracing

最暴力的光线追踪算法，是对第一个intersection point，都发射出大量的随机方向光线（每一条光线又会产生大量递归光线），所有光线返回的radiance加权平均就是该点的radiance。

这样需要发射的光线太多，计算量太大。

而路径追踪，从屏幕像素出发的光线不会分裂，当然代价就是噪声会很大，有多种降噪方法，一种是从屏幕像素发射不止1条光线而是N条（每条依然不分裂），然后算平均值；一种是用类似TAA的temporal filter方法， 每一帧做次像素jitter，并混合历史帧实现超采样。

双向路径追踪

这是一种更高效的路径追踪算法。包括了两方面：

• Backwards Path Tracing。从屏幕射出光线，到达光源时终止。
• Light Tracing (or Forwards Path Tracing)。从光源射出光线，到达屏幕时终止。

算法关键点

假设开发一个基于path tracing积分器、输入为mesh模型、包含几种基本材质的离线渲染器，下面是需要掌握的点。

每个像素的光线发射流程

1. 根据该像素的屏幕坐标、摄像机空间位置，算出Ray的o和d
2. 初始化Li为Color::Black。Li是指这根光线最终返回时收集到的Radiance，因为假设场景中没有光源（自发光物体认为是区域光源），那么场景必然是黑的。
3. 初始化pathThroughput为Color::White。pathThroughput大概就是指反射率，但是是要累乘的，每次光线反弹，要不断乘以材质的反射率。
4. 开始进入无限递归Loop（物理上也可认为光线能无限弹射）
   1. Scene.Intersect(ray)，光线和场景做相交判定。
   2. 如果不相交，那么 Li += pathThroughput * 环境贴图的Radiance（非必要功能，且这里面很复杂），并退出循环，否则继续后续步骤
   3. Li += pathThroughput * 相交点的自发光Radiance（区域光）
   4. 根据相交点的BSDF是不是specular

空间加速结构

现在显卡从硬件上支持了空间加速结构，软渲的话直接找个BVH的开源实现比较省事，也方便后面直接移植GPU。不过要注意传给BVH的ray的起点坐标，要沿着ray的朝向偏移一点点，不然可能会自相交。

几何数学

Barycentric Coordinates 和 Cramer's rule

bvh intersect的结果如果只返回了距离t，那么只能知道碰撞点P在ray.o + t * ray.d，并不能知道P点的法线。

法线有两种情况：

1. mesh没有顶点法线。这种可以根据3个顶点坐标，叉积算出面法线，P点的法线和面法线一样。
2. mesh有顶点法线。此时需要根据P点的Barycentric Coordinates，插值得到P点法线。

Barycentric Coordinates，除了用面积法算之外，还可以用Cramer's rule（克莱姆法则）算（更快）：

void Barycentric(const Vector3& hitPoint, float& u, float& v, float& w) const
{
    /*
    P_hit = p_1 + u * (p_2 - p_1) + v * (p_3 - p_1)
    u * (p_2 - p_1) + v * (p_3 - p_1) = P_hit - p_1
    B = p_2 - p_1
    C = p_3 - p_1
    A = P_hit - p_1
    =>
    u * B + v * C = A   （it is vector！）
    convert to linear system =>
    (u * B + v * C)·B = A·B       （it is scalar！）
    (u * B + v * C)·C = A·C

    u * B·B  +  v * C·B = A·B
    u * B·C  +  v * C·C = A·C

    【 B·B  C·B 】 【 u 】   A·B
    【 B·C  C·C 】 【 v 】 = A·C

    【 d00  d01 】 【 u 】   d20
    【 d01  d11 】 【 v 】 = d21

    det   = | d00  d01 |
            | d01  d11 |

    det_u = | d20  d01 |
            | d21  d11 |

    det_v = | d00  d20 |
            | d01  d21 |
    */
    Vector3 B = point_[1] - point_[0], C = point_[2] - point_[0], A = hitPoint - point_[0];
    float d00 = B.dot(B);
    float d01 = C.dot(B);
    float d11 = C.dot(C);
    float d20 = A.dot(B);
    float d21 = A.dot(C);
    float denom = d00 * d11 - d01 * d01;
    float denom_u = d20 * d11 - d01 * d21;
    float denom_v = d00 * d21 - d20 * d01;
    float inv_denom = 1 / denom;
    float u1 = denom_u * inv_denom;
    float v1 = denom_v * inv_denom;
    // P_hit = p_1 + u * (p_2 - p_1) + v * (p_3 - p_1)
    // =>
    // P_hit = (1 - u - v) * p_1 + u * p_2 + v * p_3 
    u = 1 - u1 - v1;
    v = u1;
    w = v1;
}

（参考：https://ceng2.ktu.edu.tr/~cakir/files/grafikler/Texture_Mapping.pdf ）

这个一般的

用俄罗斯轮盘赌算法（Russian Roulette）终止递归

先复习一个概念：数学期望E。

数学期望是指，每次可能的结果乘以其结果概率的总和。

例如丢骰子游戏，每个面出现的概率是1/6，那么丢出来的结果数学期望是多少呢？

\[ E(X) = 1 \cdot \frac{1}{6} + 2 \cdot \frac{1}{6} + 3 \cdot \frac{1}{6} + 4 \cdot \frac{1}{6} + 5 \cdot \frac{1}{6} + 6 \cdot \frac{1}{6} = 3.5 \]

在路径追踪中计算Radiance时，需要算每个intersection point的Radiance，实际上算的也只是Radiance的数学期望，假设Radiance的取值只有两种：Lo或者0，Lo是指继续沿着光线路径，追踪得到的Radiance值；而0则是终止追踪返回的值（纯黑色）。设继续追踪的概率为P，终止追踪的概率为1-P。

于是Radiance的数学期望为：

\[ E = Lo \cdot P + 0 \cdot (1 - P) = Lo \cdot P \]

可以看到，E和Lo不等，且比值为P。这个P可以巧妙地干掉，只需要改下公式：

\[ E = \frac{Lo}{P} \cdot P + 0 \cdot (1 - P) = Lo \]

因为P是递归的概率，只要P小于1，那么就不可能无限递归。

光源

光源数据结构问题

光源是point light（无体积）。

光源是一个三角面片模型，那么采样光源时，需要随机采样光源投影后的面积上的点，比较复杂。

光源是area light，即一个quad面片，做采样也不会太复杂。

光源是方向光，Emmm。

光源远或面积过小时，采样不足

均匀随机的光线，很难命中过小的光源，就会产生很强烈的噪点。解决该问题的办法叫emitter sampling，即从intersection point直接发射一条到光源的光线。因为光源有面积，所以目标点不是光源原点，而是需要在光源面积范围上随机出一个目标点，从而得到随机化的光线方向。

光源被遮挡问题

上面说的emitter sampling，是假设了intersection point和光源之间无遮挡。如果存在遮挡，那么不应该直接采样获得光源的Radiance。为了避免这个问题，需要搜索下BVH，判断是否有遮挡，有的话终止。

重要性采样

在一些简单的光线追踪代码中，一般只实现了diffuse材质，并且声明实现了Cosine importance sampling。其实对于diffuse材质来说，重要性采样就是cos，方向越接近法线，cos就越大，采样率应该越底。所以他们这个feature很简单就加上了。。

材质问题

dielectrics

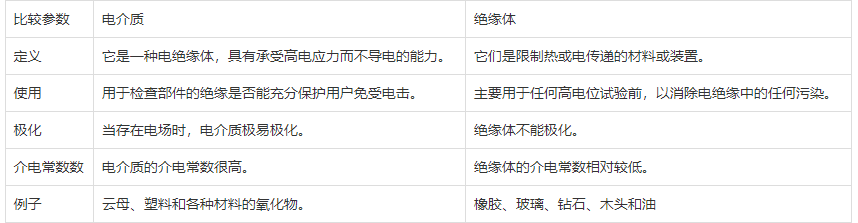
即电介质， 或称 non-metallic surfaces

电介质大部分是固体，包括：瓷器，玻璃，塑料，氧化后的金属；液体包括：水、油；气体包括：空气、氮。

纯水是电介质，不纯的水可以导电（变成了导体）。

电介质（dielectrics）不完全等于绝缘体（insulators）。

电介质和绝缘体之间的区别在于，在电场中存储或保存电能的材料是电介质材料，而在另一方面，阻止电场中电子流动的材料是绝缘体。

conductors

即导体，或称 metallic surfaces

材质细分

• 粗糙材质（LambertianDiffuse）
• 镜面材质（Mirror）
• 电介材质（Dielectric/Glass）

高级材质：

• 粗糙导体（RoughConductor)
• 粗糙电介质（RoughDielectric)
• 迪士尼材质（Disney）
• 次表面材质

材质的不同，不止是参数不同，往往代码都是差了十万八千里。

BSDF、BRDF、BTDF

BSDF 是 BRDF和BTDF的统称。

BSDF这个东西其实就是个系数。

电介材质问题

折射率 Refractive index （IOR）

折射率描述了光在电介质中的速度和真空里的速度的比值。

例如水是1.333，表示光在真空的速度比在水里的速度快1.33倍；玻璃则是1.5。

斯涅尔定律Snell's Law 和全内反射Total Internal Reflection

斯涅尔定律是用来算光经过不同介质时的折射方向的，前提是知道2个介质的折射率。

\[ η⋅sinθ=η′⋅sinθ′ \]

η、η′、sinθ是已知信息，sinθ′是要求的值。变换下上式：

\[ sinθ′=\frac {η}{η′}⋅sinθ \]

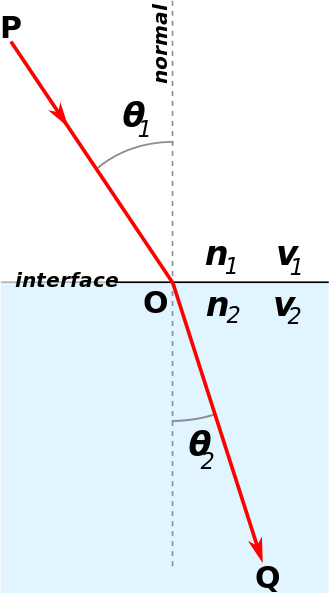
全内反射：当光线经过两个不同折射率的介质时，部分的光线会于介质的界面被折射，其余的则被反射。但是，当入射角比临界角大时（光线远离法线），光线会停止进入另一界面，全部向内面反射。

根据上面的公式可以理解这个问题，当η大于η'时，\( \frac {η}{η′}⋅sinθ \) 可能会大于1，而sin取值范围是[-1,1]，这就导致了sinθ′无解。

于是就有了一个叫临界角的概念，当θ大于临界角时，光只能反射而不能折射。临界角的计算推导：

假设\( θ_{c} \)是临界角，那么有：

\[ \frac {η}{η′}⋅sinθ_{c} = 1 \]

转换一下位置：

\[ sinθ_{c} = \frac {η′}{η} \]

\[ θ_{c} = arcsin(\frac {η′}{η}) \]

当实现电介材质（水、玻璃）时，需要考虑全内反射问题。

菲涅耳反射率 Fresnel Reflectance

上面只解决了光通过电介质时的折射方向，但是究竟多少能量被折射（以及剩下多少能量反射），是不知道的。

假定反射率为x，那么根据能量守恒可以知道折射率为1-x。

反射率一般用近似公式算(Schlick's approximation)。

用俄罗斯轮盘赌算法（Russian Roulette）算期望

这里用这个轮盘赌可以理解成减少光线分裂数。这是因为光经过不同介质时，只要不是全内反射，那么必然会分裂成2个光线，假设整个场景都是各种电介质，那么path tracing跑一遍就很慢了。

于是要引入轮盘赌：要么折射要么反射，没有光线分裂。并且利用了除以P的技巧，使得能量守恒。