首先强推大神的文章:
(Note:里面有些图片要上梯子才能加载,chart.googleapis.com,你懂得)
RSA加密/解密
需要用到的数论知识
每个正整数n都能够被分解成多个质数的乘积
\[ n = p_{1}^{ a_{1} } p_{2}^{ a_{2} } \cdots p_{k}^{ a_{k} } \]
这个分解是唯一的。不过质因子的乘积顺序可以变。质因子可以重复出现。
全等关系式
当2个整数a、b的差等于k个整数n的积时(k可以是任意整数):
\[ a - b = kn \]
可以写成:
\[a \equiv b (mod \ n) \]
例如a = 9,b = 1,n = 4时,有:
\[ a - b = 9 - 1 = 2 \cdot 4 \]
\[ 9 \equiv 1 (mod \ 4) \]
欧拉函数(Euler's function)
\[ \phi (n) = \prod _{k=1}^{ \infty } ( 1 - n^{k} ) \]
\( \phi (n) \)的含义是:在小于等于n的正整数之中,有\( \phi (n) \)个数与n构成互质关系。
这条公式深究起来是蛮复杂的。简单地去理解,其实是这么一个公式:
\[ \phi (n) = n ( 1 - \frac{ 1 }{ p_{1} } ) ( 1 - \frac{ 1 }{ p_{2} } ) \cdots ( 1 - \frac{ 1 }{ p_{k} } ) \]
\( p_{1} \ p_{2} \cdots p_{k} \) 就是上文说的质因数分解了。注意,这些质数是不能重复的,每个不同的p只会在\(\phi (n) \)公式里出现一次。
- 特殊情况1,当n为质数时,质因数分解得到1和n,1不算,那么\( \phi (n) \)简化成:
\[ \phi (n) = n ( 1 - \frac{ 1 }{ n } ) \]
\[ \phi (n) = n - \frac{ n }{ n } = n - 1 \]
- 特殊情况2,当n为2个质数p、q的积时:
\[ \phi (n) = \phi (pq) = (pq) ( 1 - \frac{ 1 }{ p } ) ( 1 - \frac{ 1 }{ q} ) \]
\[ \phi (pq) = ( p - \frac{ p }{ p } ) ( q - \frac{ q }{ q} ) \]
\[ \phi (pq) = ( p - 1 ) ( q - 1 ) \]
实例:
\( \phi (1) = 0 \)
\( \phi (2) = 2 ( 1 - \frac{ 1 }{ 2 } ) = 1,互质数为:1 \)
\( \phi (3) = 3 ( 1 - \frac{ 1 }{ 3 } ) = 2,互质数为:1、2 \)
\( \phi (4) = 4 ( 1 - \frac{ 1 }{ 2 } ) = 2,互质数为:1、3 \)
\( \phi (5) = 5 ( 1 - \frac{ 1 }{ 5 } ) = 4,互质数为:1、2、3、4 \)
\( \phi (6) = 6 ( 1 - \frac{ 1 }{ 2 } )( 1 - \frac{ 1 }{ 3 } ) = 2,互质数为:1、5 \)
\( \phi (7) = 7 ( 1 - \frac{ 1 }{ 7 } ) = 6,互质数为:1、2、3、4、5、6 \)
\( \phi (8) = 8 ( 1 - \frac{ 1 }{ 2 } ) = 4,互质数为:1、3、5、7 \)
\( \phi (9) = 9 ( 1 - \frac{ 1 }{ 3 } ) = 6,互质数为:1、2、4、5、7、8 \)
资料:
https://artofproblemsolving.com/wiki/index.php?title=Euler%27s_totient_function
https://www.geeksforgeeks.org/eulers-totient-function/
欧拉定理(Euler's theorem)
对于任意的互质的2个正整数a和n,都满足以下全等关系式:
\[ a^{\phi (n) } \equiv 1 (mod \ n) \]
证明:TODO
费马小定理(Fermat's little theorem)
这个是欧拉函数的特殊情况1的应用:若正整数n还是个质数,把n记为p,那么有:
\[ \phi (p) = p - 1 \]
代入欧拉定理公式,得到:
\[ a^{ p - 1 } \equiv 1 (mod \ p) \]
这就是费马小定理。
模逆元(Modular multiplicative inverse)
当2个正整数a和n互质时(Note:a、n本身不一定是质数),必然存在一个整数x,使得:
\[ ax \equiv 1 (mod \ n) \]
x就是所谓的模逆元。另外限定x取值范围为(0, n-1],就使得模逆元x是唯一的。
x的存在性证明:
可以用欧拉定理来证明,因为a和n互质,所以有:
\[ a^{\phi (n) } \equiv 1 (mod \ n) \]
对左边转换一下:
\[ a\cdot a^{\phi (n) - 1 } \equiv 1 (mod \ n) \]
显然,模逆元x的其中一个解等于:
\[ x = a^{\phi (n) - 1 } \]
这个解可能会超过限定范围,得做模运算才能得到真正的模逆元:
\[ x = a^{\phi (n) - 1 } (mod \ n) \]
直接用这条公式计算x,据说比较慢,更快速的算法是用扩展欧几里得算法。
中文wiki有更详细的例子:扩展欧几里得算法。
RSA加密解密原理
准备
用户首先任意选择2个质数p、q,并计算p、q乘积n:
\[ n = pq \]
然后应用欧拉函数的特殊情况2公式:
\[ \phi (n) = (p - 1)(q - 1) \]
这2个值算出来时,就可以彻底删除p、q了。后面的计算步骤和原始的p、q无关。
接着,用户随机选择一个正整数e,e的取值范围为\( [1, \phi (n)] \)。
e确定后,计算关于\( e、\phi (n) \)的模逆元d:
\[ ed \equiv 1 (mod \ \phi (n) ) \]
此时,用户总共持有4个对象:
- \( n \)
- \( \phi (n) \)
- \( e \)
- \( d \)
其中的(e、n)组成了RSA算法的公钥;(d, n)组成了私钥。
现在举个栗子来理解上面的流程:
假设p、q分别为61、53,则\(n、\phi (n) \)分别等于:
\( n = 61 \cdot 53 = 3233\)
\( \phi (n) = (61 - 1) (53 - 1) = 3120 \)
e选择17(在范围[1,3120]内即可),并算出d:
\( d = 2753 \)
(用扩展欧几里得算法计算得到)
所以公钥为(17, 3233),私钥为(2753, 3233)。
加密
假设用户A把公钥(e,n)给到用户B,让用户B给他发送一个原文信息m,m为一个数字。
原文m的加密过程如下:
\[ m^{e} \equiv c ( mod \ n) \]
用上面的例子来理解:假设m为65,公钥为(e,n)(17, 3233),则有:
\[ 65^{17} \equiv 2790 (mod \ 3233) \]
密文c等于2790。
解密
解密流程就不太好理解了,先搬出公式:
\[ c^{d} \equiv m (mod \ n) \]
代入密文c 2790和私钥(d,n)(2753, 3233),算出原文m:
\[ 2790^{2753} \equiv 65 (mod \ 3233) \]
这样就算出了原文m,是不是和变魔术一样。
分析小结
- 因为要对原文m做模n运算,意味着原文m是不能超过n的,不然取模前后的值是不一致的,就达不到加密解密效果
- 解决办法是对原文m切成多段m1、m2、m3,每一段都小于n,对每一小段加解密(分组加密)
- 另一种办法是,不直接用RSA对原文加解密,而是用别的对称加密算法如AES对原文加解密,RSA只用来加密AES对称密钥
解密公式的数学依据
前面的内容,并没有提到为什么以下这条公式可以保证解出原文m:
\[ c^{d} \equiv m (mod \ n) \]
这需要做一番推导才能理解。
首先,搬出加密公式:
\[ m^{e} \equiv c ( mod \ n) \]
从加密公式开始推导(以下等式都隐含\(mod \ n\)操作):
\[ c \equiv m^{e} \] \[ c^{d} \equiv m^{ed} \] \[ c^{d} \equiv m^{1 + k(p - 1)(q - 1) } \] \[ c^{d} \equiv m\cdot m^{ k(p - 1)(q - 1) } \] \[ c^{d} \equiv m\cdot (m^{ (p - 1)(q - 1) })^{ k } \] \[ c^{d} \equiv m\cdot (1)^{ k } \] \[ c^{d} \equiv m\]
得证 \( c^{d} \equiv m (mod \ n)\)
其中不好理解的是第2行到第3行、第5行到第6行。
第2行到第3行的原理:
\[ ed \equiv 1 (mod \ \phi (n) ) \]
\[ ed = 1 + k\phi (n) \]
\[ ed = 1 + k(p - 1)(q - 1) \]
第5行到第6行的原理是欧拉定理:
\[ m^{\phi (n) } \equiv 1 (mod \ n) \]
\[ m^{ (p - 1)(q - 1) } \equiv 1 (mod \ n) \]
RSA算法的可靠性保证
公钥是(e,n),私钥是(d,n),攻击者唯一能知道的只有公钥(e,n),那么攻击者是否能算出d,得到私钥(d,n)呢?
破解d的思路:
- \( ed \equiv 1 (mod \ \phi (n) ) \),只有知道e和\(\phi (n) \),才能算出d;
- 而 \( \phi (n) = (p - 1)(q - 1) \),只有知道p和q,才能算出\(\phi (n) \);
- 而 pq = n。只有对n做质因数分解,才能算出p和q。
所以,能否在短时间内对n做分解得到p、q,是RSA算法是否可靠的关键。目前来说,还没有快速地求质因数分解的算法。
针对RSA加密/解密的攻击问题
上面的加密解密公式:
\[ m^{e} \equiv c ( mod \ n) \]
\[ c^{d} \equiv m (mod \ n) \]
可以用函数R表达:
\[ c = R(m, e) \]
\[ m = R(c, d) \]
对于同一个RSA加密解密函数,输入同样的原文,就会输出同样的密文,这就给了攻击者可乘之机。攻击者如果观察到有2个密文是一样的,就有可能推导出关于此次通讯的更多信息。
解决办法是增加前后处理:
\[ c = R(preprocess(m), e) \]
\[ m = postprocess(R(c, d)) \]
这种前后处理方法被叫做padding schemes,但并不只是做padding。
这类方法最常见的是OAEP,optimal asymmetric encryption padding(1994年):
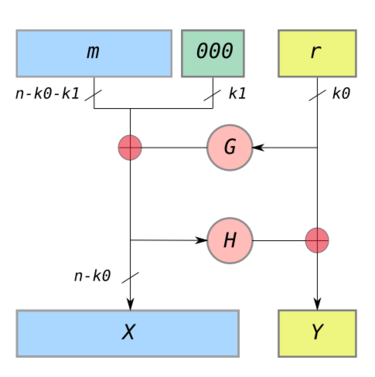
OAEP-pre(m):
- r = random nonce
- X = (m || 00...0) XOR G(r) // pad m with zeros
- Y = r XOR H(X)
- output:m' = X || Y
OAEP-post(m'):
- split m' into X || Y
- r = Y XOR H(X)
- (m || 00...0) = X XOR G(r)
- output m
G、H是典型的某种加密学哈希函数。
综上,RSA-PAEP的加密解密公式如下:
\[ c = R(OAEPpre(m), e) = R(m', e) \]
\[ m = OAEPpost(R(c, d)) = OAEPpost(m') \]
wiki的这张图非常清晰地诠释了OAEP的处理过程:
参考资料:
RSA数字签名
RSA数字签名就是RSA加密的逆
签名过程,用私钥k加密原文m:
\[ c = R(m,k) \]
验证签名过程,用公钥解密密文c得到m',验证m'是否等于m:
\[ R(c,K) == m \]
只有持有私钥的人才可以做签名,每个获得公钥的人都可以做验证。签名/验证签名的一个特点是,原文m是暴露的,没有秘密可言。
RSA签名的问题
原文m长度超过上限n
此时,可以对m做哈希,算出来的摘要控制在n长度内:
\[ c = R(H(m), k) \]
\[ c = R(s, K) == H(m) \]
里面H可以用上面的OAEP里的H算法。
然而这个流程也只是最简单的RSA数字签名方案,还有更完善的PSS。
RSA-PSS
RSA-PSS(Probabilistic Signature Scheme),基于概率的RSA数字签名方案。
参考资料
https://www.cs.cornell.edu/courses/cs5430/2015sp/notes/rsa_sign_vs_dec.php
https://blog.csdn.net/qq_34911465/article/details/78790377
https://pdfs.semanticscholar.org/b459/5fffe0562776a2830c7b525ba9f641110d7a.pdf
写作不易,您的支持是我写作的动力!