ECC算法
直观认识什么是椭圆曲线
椭圆曲线,指的是满足这个维尔斯特拉斯通用式的曲线:
\[ y^{2} = x^{3} + ax + b , 且 4a^{3} + 27 b^{2} ≠ 0 \]
判别式(discriminant )不为0时,曲线才没有奇异点,才能用于加密。
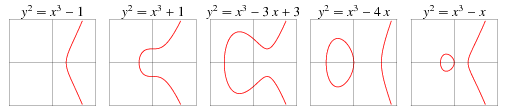
到这里就能发现椭圆曲线第一个特点:整个曲线是关于x轴对称的。
各类加密货币使用的椭圆曲线代号是secp256k1,长这样子:
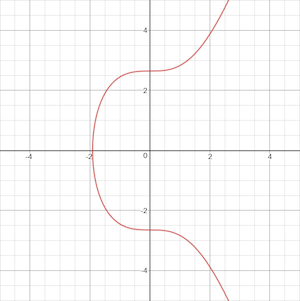
用这个在线工具可以打印椭圆曲线:
import numpy as np
import pylab as pl
def f(x):
return x**3 - x # 替换掉这个方程,然后重新run
Y, X = np.mgrid[-10:10:100j, -10:10:100j]
pl.contour(X, Y, Y**2 - f(X), levels=[0])
pl.show()
ECC算法细节
曲线基本特点
- 如果一条(不垂直于x轴的)直线与椭圆曲线相交(有2个相交点),那么必然存在第三个相交点。(证明过程?)
- 第三个点相当于公钥
- 椭圆曲线关于x轴镜像对称
无穷远点0 Point at infinity
无穷远点,或理想点,指理想化地认为一条直线在无穷远处有一个终点,一般以0表示。
椭圆曲线上的点的取反操作
因为椭圆曲线关于x轴对称,所以可定义:
对于任意椭圆曲线上的点P,对P取反后得到-P,-P为P关于x轴镜像对称点。
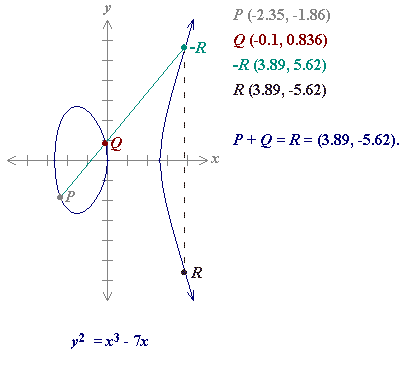
P + Q = R
前面已经提到,任意直线与椭圆曲线如果相交,那么必然有3个相交点。(记得相交线不能和x轴垂直)
在椭圆曲线加密算法中,定义了一个阿贝尔群,该群的的加法操作定义如下:
对于任意相交点P、Q、-R(这里取反是有意义的),若P!=-Q,有等式 P + Q + (-R) = 0 成立,即 P + Q = R。
- 首先要注意,这个加法并不是欧氏几何加法,例如看下图, P + Q在欧氏几何中的结果是(-2.45,-1.024),而不是(3.89,5.62)
- 该定义中,要求P!=-Q,也是有深意的:如果P=-Q,说明P和Q是关于x轴对称的2个点,那么P和Q应是R和-R,所以P!=-Q这个前提条件保证了P和Q不是那个特殊的R
base point P
在椭圆曲线加密算法中,第一步是定一个基准点P。
第二步是,找出从P到P的直线方程。此时会疑惑2个一样的点怎么构成直线,当然是可以的,这个直线是经过P点的和椭圆曲线相切的切线:
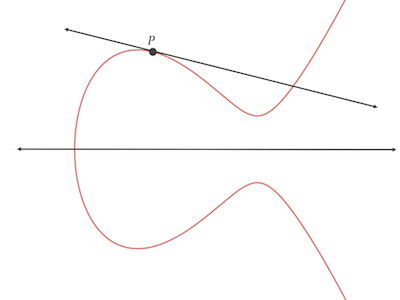
根据前面小节的说明,这条切线必然会与椭圆曲线相交于另外一点-R,又因为P + Q = R(-R的镜像点),所以有 P + P = 2P = R:
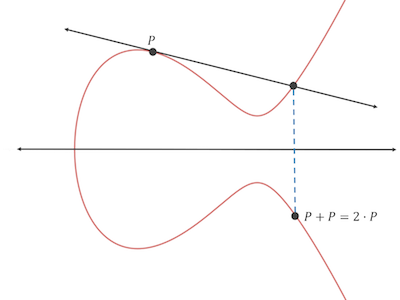
这一个过程还可以迭代下去:因此此时已有P和2P两个点,如果让它们相加,即 P + 2P,那么又会得到新的一个镜像点3P:
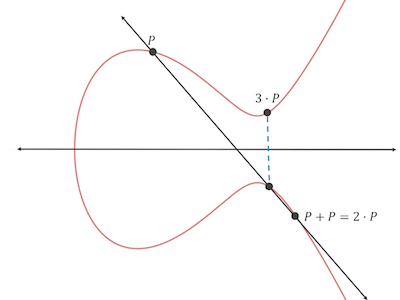
继续迭代这个过程,就能得到4P、5P、6P······
nP + rP = (n+r)P
假设现在要求出10P,那么按上一节的迭代算法,就需要计算:
\[ P+P+P+P+P+P+P+P+P+P \]
这是很慢的过程,不过可以用群加法其中一个性质来加速:
\[ nP + rP = (n+r)P \]
当然还是不能一步到位,而是从9次加法变成了4次加法:
\[ P + P = 2P \]
\[ 2P + 2P = 4P \]
\[ 4P + 4P = 8P \]
\[ 2P + 8P = 10P \]
x为大数时,xP的计算问题
假设x是一个超大正整数,例如有256bits,32个字节这么大。那么要得到xP,得做多少次群加法呢?
这是个二进制的问题。首先假设x等于十进制的246(值很小,只用一个字节就能表示,是为了讨论方便),并把x二进制展开(binary expansion,是叫二进制展开吧?):
\[ 2^{7} + 2^{6} + 2^{5} + 2^{4} + 2^{2} + 2^{1} = 128 + 64 + 32 + 16 + 4 + 2 = 246 \]
等式两边都乘以P:
\[ 2^{7}P + 2^{6}P + 2^{5}P + 2^{4}P + 2^{2}P + 2^{1}P = 246 P \]
此时x=246的xP问题就解决了:先算出一系列\(2^{n} P\),n从0到255(255次群加法),然后用5次群加法就得到了246P,总共需要260次群加法。
当x的256bits都为1,即x取最大值时,也只需要做255+255=510次群加法。
逆向求xP的x
假设Bob和Alice玩一个椭圆曲线的游戏:Bob先保密地随机取一个256bits的x,并算出X = xP,把X点坐标告诉Alice;Alice也知道这个椭圆曲线方程以及P点,那么Alice是否可以求出x的值?
再复述下Alice掌握的信息:
- 椭圆曲线方程,如:\(y^{2} = x^{3} - 7x \)
- P点坐标,如:(-2.35, -1.86)
- X点坐标,如:(123.456,789.123)(瞎写的)
Alice是否可以知道X是做了多少次对P的群加法得到的?如果能,需要多久?
答案是,现在世界上并没有一个快速算法求出x。唯一可行的笨办法是,遍历整个256bits范围的整数集,从1P开始,不断+P,直到发现nP=X,此时的n就是要求的x。
也有同样复杂度的逆算法:不断对X减P,直到减完时刚好就是P,此时统计减的次数,就是x了。
x落在\( [0, 2^{256} - 1] \),平均值为\( 2^{128} \)。因此平均需要暴力地做2128次群加法。
公钥私钥
基于上一节的讨论,x和X适合用来做非对称加密的私钥公钥:
- 私钥:大数x
- 公钥:椭圆曲线上的坐标X
非对称加密的公钥私钥必然要满足一个性质:给定一个公钥,很难去推导出它对应私钥。可见,x和X满足这个性质。
但X、x公钥私钥对并不能直接用于加密数据。这个事情后面再说。
谁才是主人公?持有私钥证明 part1
Bob持有私钥x,是事实,但Bob怎么向别人证明自己持有X对应的私钥x呢?
这个事情有点复杂,首先要改进下椭圆曲线的模型。
上面的椭圆曲线模型有个问题:xP这个点的坐标x、y可能会超大,x和y加起来可能大过一个公钥的存储极限,例如512bits。
解决方案是:在有限域上定义一个椭圆曲线。为此有2个新的限制:
- 坐标点的分量限制为整数
- 坐标点的分量取值范围不是无穷远
公式上的改变如下:
把 \( y^{2} = x^{3} + ax + b\) 改成:
\[ ( y^{2} ) \% p = ( x^{3} + ax + b ) \% p\]
p是一个大质数,例如在secp256k1椭圆曲线中,p的取值是【0, \( 2^{256} \) 】范围内的最大质数。
这么一转换后,椭圆曲线就变成大概这样子的东西:
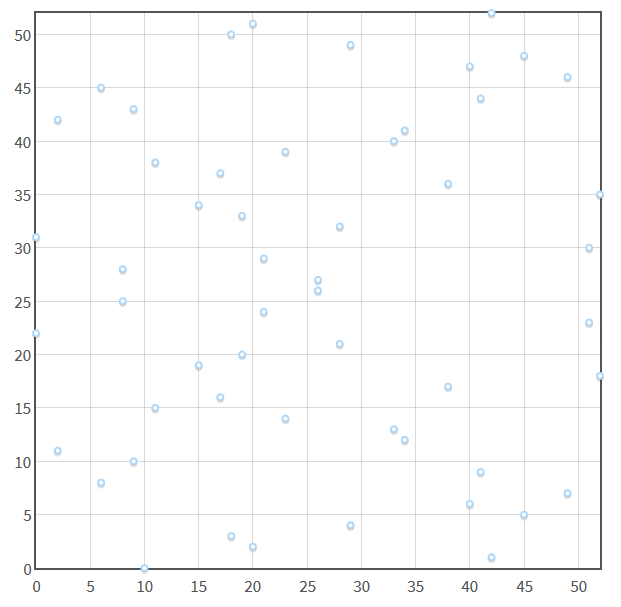
离散的点集,但仍然有关于x轴的对称性。
而且,前面讨论的东西仍然是有效的。
谁才是主人公?持有私钥证明 part2
如何才能在不暴露x的前提下告诉别人“我”持有私钥呢?
首先拿出前面提到的加法结合律:
\[ n \cdot P + r \cdot P = ( n + r ) \cdot P \]
然后把n替换为这个东西:
\[ hash(m, \ r \cdot P) \cdot n \]
得到:
\[ hash(m, r \cdot P) \cdot n \cdot P + r \cdot P = ( hash(m, r \cdot P) \cdot n + r ) \cdot P \]
引入了一个新的m,以及关于m和rP的hash函数。
假设\(n \cdot P = X \)(X就是公钥X),代入上式,得到:
\[ hash(m, r \cdot P) \cdot X + r \cdot P = ( hash(m, r \cdot P) \cdot n + r ) \cdot P \]
又因为\(n \cdot P = X \),所以有n = x(x就是私钥x),继续代入,得到:
\[ hash(m, r \cdot P) \cdot X + r \cdot P = ( hash(m, r \cdot P) \cdot x + r ) \cdot P \]
此时再设2个新的对象R和s:
\[ R = r\cdot P \]
\[ s = hash(m, R)\cdot x + r \]
把R代入上面的方程,变成:
\[ hash(m, R) \cdot X + R = ( hash(m, R) \cdot x + r ) \cdot P \]
然后再代入s,最终得到:
\[ hash(m, R) \cdot X + R = s \cdot P (持有私钥证明方程)\]
这条方程就是持有私钥证明了:谁能够给出任意m、R、s,使得m、R、s代入上述方程使得等式成立,那么这个人就必然持有私钥x。
那么对持有人来说,怎么得到m、R、s呢?很简单:
- 随机生成m
- 随机生成r
- 计算\( R = r\cdot P \)
- 计算\( s = hash(m, R)\cdot x + r \)
这里提2个问题。一个是私钥安全问题:
对第三者来说,未知数是r和x,假设r泄露了给第三者,那么第三者就可以根据第4步的式子的变换,导出私钥x:
\[ x = \frac { s - r } { hash(m, R) } \]
所以r必须是用完就丢的。因为持有者只需要给出R就足够用予持有私钥证明。
另一个是暴力破解问题:
第三者是否可以暴力地找到合适的m、R、s代入持有私钥证明方程,使得方程成立?
假设可行,那么第一步应是先任意找出一组合适的参数:h( h = hash(m, R) )、R、s,使得\( hash(m, R) \cdot X + R = s \cdot P \) 成立,这肯定是办得到的。
然后下一步是,解出一个m,使得hash(m, R) = h成立。然而,如果选择了一个优质的cryptographic hash functions,是很难办到的。这也被称为原像攻击(Preimage attack ),即给定hash值,找出能hash出这个值得输入。
ECC的应用:数字签名(ECDSA)
前面已经论证了只有私钥持有者能给出m、R、s三元组,那么当m是一段有意义的消息(依然是一段字节序),而与这个m匹配的R、s,就成为这个消息m的签名了。
因为攻击者理论上并不能用自己随意篡改的m',使得m'、R、s能成功代入持有私钥证明方程。
ECC的应用:比特币
简单来说,要生成一个新的比特币钱包,需要先随机生成一个256bits的私钥x,然后根据比特币所用的椭圆曲线参数(secp256k1),计算X = xP,X就是这个钱包的公钥。
然后呢,X大有所为,X可以随便公开,X相当于钱包的银行账号,例如比特币转入这个钱包,就需要用到X。
转入问题是解决了,但怎么证明你是这个钱包的主人,并转出(消费)比特币呢?答案就是用上一节的方法,做一个持有私钥声明(即数字签名),转出事务广播开后,每个人都可以简单地验证这个持有声明的真伪性。
如果去观察比特币的事务消息,就会发现他它的数字签名部分就是一个椭圆曲线上的某坐标R和一个随机的256bits的s的组合。
ECC的参数集合(Elliptic Curve Domain Parameters)
纠正下前面介绍ECC相关参数的命名。
椭圆曲线算法有很多参数,被称为Elliptic Curve Domain Parameters:
- a:椭圆曲线方程\( y^{2} = x^{3} + ax + b \) 里的a
- b:椭圆曲线方程\( y^{2} = x^{3} + ax + b \) 里的b
- G:即上文说的P,椭圆曲线上任意取得基准点坐标
- p:质数p,用来控制值域范围的
- n:基准点G的阶(order),即使得nG=0(无穷远点)的最小正整数。
- h:辅因子(cofactor),h等于\( \frac {1}{n} | E(F_{p}) | \)。当h为最理想的1时,整个点群#E都可以被使用,否则,可用的点群大小只有#E/h。
可以这样理解n:nP = iP + jP = 0, 即椭圆曲线上某2个点iP、jP,它们的和nP为无穷远点,即经过iP、jP的直线垂直于x轴,当i+j=n取到最小值时,即为G点的阶。
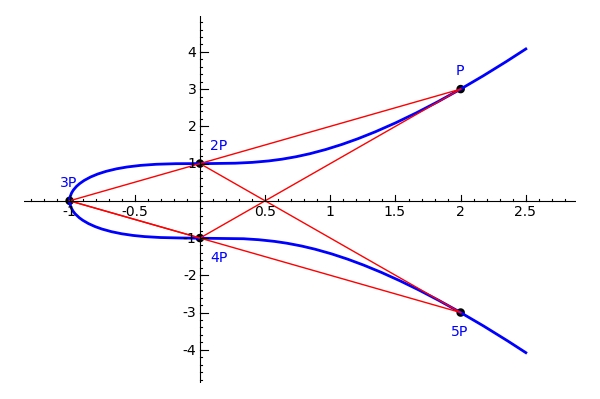
(观察此图,发现5P + P = 6P = 0,P点的阶为6。进一步阅读 )
当阶数n和#E一样大时,h取到最佳值1。h的计算,必然要先理解透彻群论的知识,这里不做展开,可以阅读这2个链接:
https://math.stackexchange.com/questions/1394251/calculating-elliptic-curve-cofactor-h
https://en.wikipedia.org/wiki/Hasse%27s_theorem_on_elliptic_curves
ECC的应用:加密通讯 ECDH
要仅仅用ECC来加密数据,那么就要用到ECIES这个。
ECIES,即基于椭圆曲线的整合加密方案,与其类似的还有基于离散对数的整合加密方案 (DLIES)。
ECIES,也被称为Elliptic Curve Augmented Encryption Scheme(基于椭圆曲线的增强加密方案) 或简单地叫 Elliptic Curve Encryption Scheme(基于椭圆曲线的加密方案)。
Anyway,先以一个例子介绍下ECIES:Alice和Bob进行加密通讯。
通讯前准备:
- 一个椭圆曲线和参数集合(p,a,b,G,n,h)
- Alice已获得Bob的公钥\( K_{B} \)。\( K_{B} = k_{B}G , k_{B} \in [1, n - 1] \), \( k_{B} \)是Bob自己随机生成的私钥。(再次注意,\( k_{B} \)是值, 而\( K_{B} \)是一个椭圆曲线上的点。)
- 双方共享信息: \( S_{1} ,S_{2}\) (nonce)
加密流程:(Alice加密原文m)
- 生成随机数r,计算R = rG
- 计算\(P = (P_{x}, P_{y}) = rK_{B} \),取P的x分量\(P_{x}\)作为共享密钥S。
- 用KDF密钥导出函数,导出定长的对称加密密钥\(k_{E} \)和MAC密钥\(k_{M} \),\( k_{E} || k_{M} = KDF(S || S_{1}) \)
- 加密消息:\( c = E( k_{E}, m) \),E代表Encrypt函数。
- 计算MAC:\( d = MAC(k_{M}, c|| S_{2}) \)
- 输出\(R || c || d\)
解密流程: ( Bob已收到\(R || c || d\) )
- Bob先求出Alice也在使用的共享密钥\(P_{x}\), \(P = (P_{x}, P_{y}) = rK_{B} = rk_{B}G = k_{B}R \),R是Alice发来的,\( k_{B} \)是本地的。
- Bob也用一样的方法求出2个密钥,\( k_{E} || k_{M} = KDF(S || S_{1}) \)
- 检查收到的d和自己算的d‘是否一致,不一致的话说明c被中间人篡改了:\( d' = MAC(k_{M}, c|| S_{2}) \)
- 此时就可以用对称加密密钥,解出消息m:\( m = E^{-1}(k_{E}, c) \) ,\(E^{-1}\)代表Decrypt函数(一般等同于Encrypt函数)。
其实这个流程就是非常著名的ECDH算法了。Alice和Bob利用ECC算法,进行了密钥交换,得到了\( P_{x} \)。
资料:
补充:已知P、Q,怎么求R
这个问题其实是解方程组问题,一个是直线的方程: \(y = kx + c\),一个是椭圆曲线的方程:\( y^{2} = x^{3} + ax + b \)。
(推荐一个在线解方程组的工具:wolframalpha )
以这幅图为例:

假设已知的只有:
- 椭圆曲线方程:\( y^{2} = x^{3} - 7x \)
- P(-2.35089, -1.86107)
- Q(-0.0999884, 0.836014)
现在目标是求,直线与曲线的第三个交点R(应该叫-R)的坐标。
第一步,化解方程组:
\[ y = kx + m, y^{2} = ax^{3} + bx^{2} + cx + d \]
\[ (kx + m)^{2} = ax^{3} + bx^{2} + cx + d \]
\[ 0 = ax^{3} + (b - k^{2}) x^{2} + (c - 2km)x + d - m^{2}\]
本例的椭圆方程的系数为:
\[ a = 1, b = 0, c = -7, d = 0\]
代入上式,得到:
\[ 0 = x^{3} - k^{2}x^{2} - (7 + 2km)x - m^{2}\]
第二步,搬出韦达公式,对于一元三次方程,它的根之间有如下关系式:
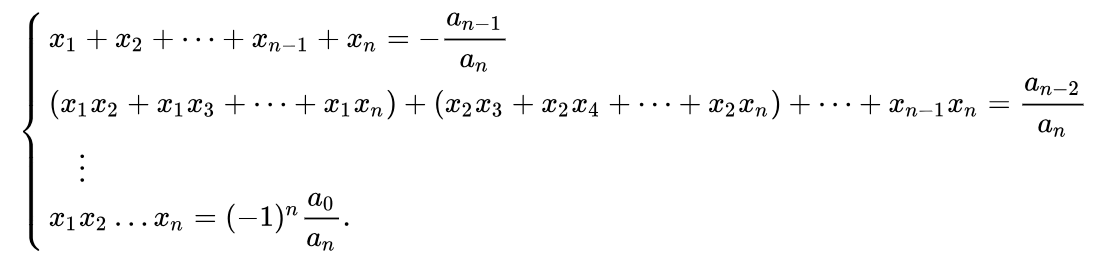
用到我们这里,就是:
\[ x_{1} + x_{2} + x_{3} = -\frac {b}{a} = -\frac { -k^{2} }{1} = k^{2} \]
\[ x_{1} * x_{2} * x_{3} = -\frac {d}{a} = -\frac { -m^{2} }{1} = m^{2} \]
\[ x_{1}x_{2} + x_{2}x_{3} + x_{1}x_{3} = \frac {c}{a} = \frac {- (7 + 2km)}{1} = - (7 + 2km) \]
又因为\(x_{1}、x_{2}、x_{3}\)其实就是\( P_{x}、Q_{x}、R_{x} \) ,所以有:
\[ R_{x} = k^{2} - (P_{x} + Q_{x}) \]
这样就求出了\(R_{x} \)。而R的y分量可以用斜率公式推出:
\[ \frac { R_{y} - P_{y} } { R_{x} - P_{x} } = k \]
\[ R_{y} = k (R_{x} - P_{x} ) + P_{y} \]
这里面还有个未知数斜率k,也是用斜率公式求出:
\[ k = \frac { Q_{y} - P_{y} } { Q_{x} - P_{x} } = 1.19822222 \]
最终的:
\[ R_{x} = (1.19822222)^{2} - ((-2.35089) + (-0.0999884)) = 3.8866148938271605 \approx 3.89 \]
\[ R_{y} = (1.19822222) (3.8866148938271605 - (-2.35089) ) + (-1.86107) = 5.6128469750035 \approx 5.61 \]
\[ -R = (3.89, 5.61),R = (3.89, -5.61) \]
和图片里的数值一样。
写作不易,您的支持是我写作的动力!

