DH算法
key exchange例子( from here ):
- Alice和Bob首先线下商量好,使用p (prime, 质数) = 23、g (generator, 生成器) = 5作为通讯基础(p和g不需要绝对的保密,泄露了也没事)
- 每次Alice和Bob想要建立通讯(连接)时,Alice自己随机生成一个在范围[1, p - 1]的数:a = 6
- 同样,Bob自己也随机一个:b = 15
- Alice计算: \( A = g^{a} \% p = 5^{6} \% 23 = 15625 \% 23 = 8 \),把A发给Bob
- Bob计算: \( B = g^{b} \% p = 5^{15} \% 23 = 30517578125 \% 23 = 19 \),把B发给Alice
- Alice收到B后,可计算出对称密钥:\( s_{Alice} = B^{a} \% p = 19^{6} \% 23 = 47045881 \% 23 = 2 \)
- Bob收到A后,可计算出对称密钥:\( s_{Bob} = A^{b} \% p = 8^{15} \% 23 = 35184372088832 \% 23 = 2 \)
数学原理
其中,用到了模幂运算的基本定理,对于任意自然数a、b、n,有:
\[ ab\ \%\ n = ( ab\ \%\ n) \ \%\ n = ( (a\ \%\ n) (b\ \%\ n) ) \ \%\ n \]
应用到幂运算:
\[ a^{b}\ \%\ n = ( a \cdots a ) \ \%\ n = ( (a\ \%\ n) \cdots (a\ \%\ n) ) \ \%\ n = ( \ (a\ \%\ n) ^{b}\ ) \ \%\ n \]
\[ a^{b}\ \%\ n = ( a^{b}\ \%\ n) \ \%\ n \]
观察这2个式子最右边,发现b的位置是可以移动的:
\[ ( \ (a\ \%\ n) ^{b}\ ) \ \%\ n = ( a^{b}\ \%\ n) \ \%\ n \]
套进上一节的例子里的推导公式,得到:
\[ s_{Alice} = B^{a} \% p = (\ (\ g^{b} \% p\ ) ^{a}\ ) \% p = ( \ g^{ab} \% p\ \ ) \% p = \ g ^{ab} \% p \]
同理:
\[ s_{Bob} = A^{b} \% p = (\ (\ g^{a} \% p\ ) ^{b}\ ) \% p = ( \ g^{ab} \% p\ \ ) \% p = \ g ^{ab} \% p \]
显然有:
\[ s_{Alice} = s_{Bob} \]
这样就协商出了对称的密钥,密钥实质等于:
\[ g ^{ab} \% p \]
其中,g、p可公开、a、b保密。
为什么可行
从攻击者角度看,攻击者最多只能获得以下信息:
- p:23
- g:5
- A:8
- B:19
攻击者目标是获得s(serect)。要计算s,就是算2条式子:
\[ s = ( B^{a} ) \% p \]
\[ s = ( A^{b} ) \% p \]
显然,攻击者只需要破解出a或b,就能得到s。
又因为有:
\[ A = ( g^{a} ) \% p \]
\[ B = ( g^{b} ) \% p \]
所以破解a或b的方法是:
\[ a = log_{g}^{A} \% p \]
\[ b = log_{g}^{B} \% p \]
这看似很简单的算术(对数运算和取模运算),其实是很难算的。目前为止没有找到一个快速计算离散对数的算法。
关键在于p这个素数要足够大,那么以现在的计算机计算速度,就很难通过A(或B)、g、p这3个参数算出a,这被称为离散对数难题。
这里需要注意,难的是离散对数,即有log和mod运算并且参数是整数;若单单只有log运算,是不难的。
p、g的选取问题
涉及到了一些数论的概念:
首先明确下:
- p必须是素数,且必须是大数(1024-2048bits),算法才安全
- g不需要是素数,且不需要很大
p、g不需要自己挑选,可以直接用rfc5114给定的值。
例如1024-bit MODP Group with 160-bit Prime Order Subgroup:
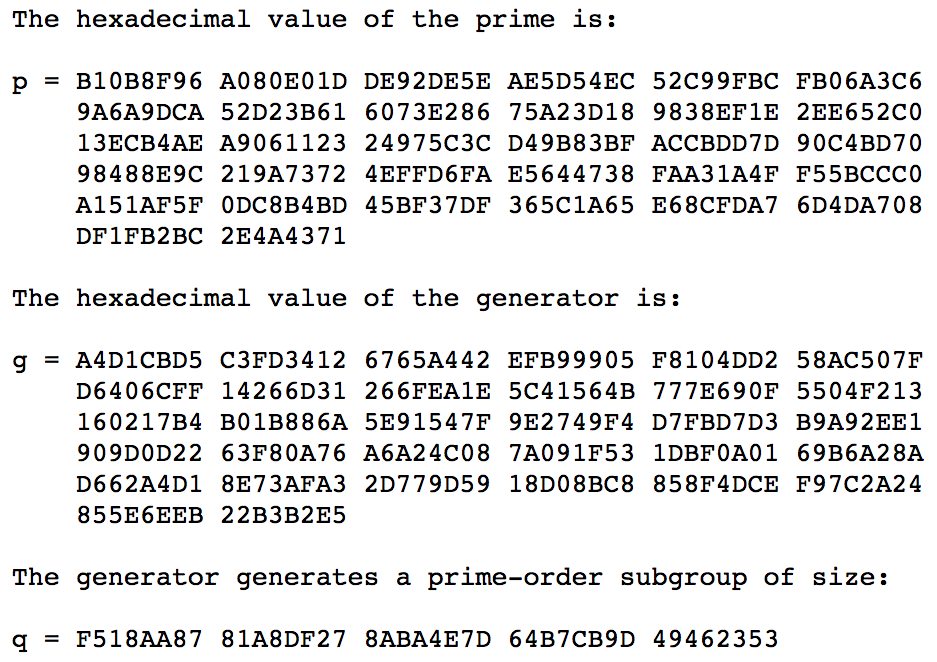
再讲下去就是深入密码学、数论了,按住不表。
写作不易,您的支持是我写作的动力!

