欧拉公式

复数和三角函数有密切的联系，因为大神欧拉发现了这样的公式：

\[ e^{ix} = \cos x + i\sin x\]

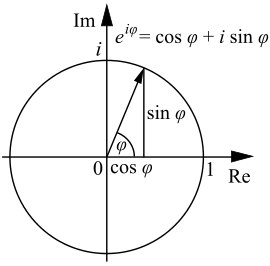
(图片来自 wikipedia-Euler-formula)

怎么推导出欧拉公式?

设z是复数平面的一个复数，且用三角函数来表示它的实数和虚数：

\[ z = \cos \theta + i\sin \theta \]

两边算微分:

\[ dz = (-\sin \theta + i\cos \theta)d\theta \]

提取i:

\[ dz = i( \cos \theta + i\sin \theta )d\theta \]

注意看，括号内的东西，不就是z嘛，所以有:

\[ dz = izd\theta \]

换个写法:

\[ \frac {1}{z}dz = id\theta \]

两边求积分:

\[ \int_{}^{} \frac {1}{z}dz = \int_{}^{} id\theta \]

\[ \ln z = i\theta \]

注意，右边的积分，是把i当做常数看待的，所以i直接被提取出来。

再写出这个式子的指数形式:

\[ e^{\ln z} = e^{i\theta } \]

\[ z = e^{i\theta } = \cos \theta + i\sin \theta \]

推导完毕。

欧拉公式的延伸特性

由:

\[ e^{ix} = \cos x + i\sin x\]

得到:

\[ e^{-ix} = \cos (-x) + i\sin (-x) = \cos x - i\sin x \]

上面两个等式相加:

\[ e^{ix} + e^{-ix} = (\cos x + i\sin x) + (\cos x - i\sin x) \]

\[ = 2\cos x \]

所以有:

\[ \cos x = \frac {e^{ix} + e^{-ix}}{2} \]

同样的，把上面2个等式相减:

\[ e^{ix} - e^{-ix} = (\cos x + i\sin x) - (\cos x - i\sin x) \]

\[ = 2i\sin x \]

所以有:

\[ \sin x = \frac {e^{ix} - e^{-ix}}{2i} \]

(未经授权禁止转载)