HLBVH
上一篇文章介绍了recursiveBuild函数,它对静态场景做了一次自顶向下的BVH构造,且使用了一个叫SAH的切分技术。
recursiveBuild有2个缺点:
SAH的计算是\(O(n^{2}) \)的,且几乎每一个节点都要做SAH,性能并不是很理想;
自顶向下地构造BVH,很难应用并行计算来优化性能。
于是作者又发明了更复杂的HLBVHBuild,即 Hierarchical Linear Bounding Volume Hierarchy。
莫顿码 Morton Code
要理解HLBVH,首先要学一下莫顿码。
LeftShift3
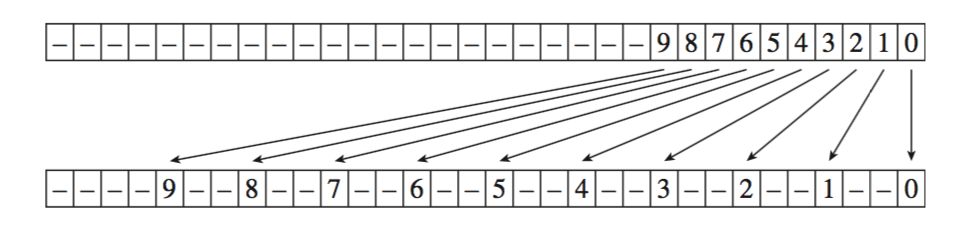
LeftShift3函数: 输入一个32位正整数(这个数实际上必须小于等于1<<10即1024),函数会把第i位的值写入到第3i位,然后把其他无关的位清0。
因为输入的数小于等于1<<10,即只有10个有效bit[0,1,2,···,9],最大的是第9bit,9*3=27,所以27bit之后的最后4个bits [28, 29, 30 ,31],必然都是0。下面函数的注释也已标明。
示意图:
(from pbrt v3)
实现代码如下,用了位运算技巧,需要慢慢理解(看注释,每一轮变换都是一次分隔,变换后都给出了有效位的新位置):
inline uint32_t LeftShift3(uint32_t x) {
Assert(x <= (1 << 10));
if (x == (1 << 10)) --x;
x = (x | (x << 16)) & 0b00000011000000000000000011111111;
// x = ---- --98 ---- ---- ---- ---- 7654 3210
x = (x | (x << 8)) & 0b00000011000000001111000000001111;
// x = ---- --98 ---- ---- 7654 ---- ---- 3210
x = (x | (x << 4)) & 0b00000011000011000011000011000011;
// x = ---- --98 ---- 76-- --54 ---- 32-- --10
x = (x | (x << 2)) & 0b00001001001001001001001001001001;
// x = ---- 9--8 --7- -6-- 5--4 --3- -2-- 1--0
return x;
}
EncodeMorton3
理解了LeftShift3后再来理解EncodeMorton3就很简单了,就一行代码:
(LeftShift3(v.z) << 2) | (LeftShift3(v.y) << 1) | LeftShift3(v.x);
调用了三次LeftShift3,分别输入了向量v的x、y、z分量。因为LeftShift3作用是用2个0bit分割有效位,所以EncodeMorton3里,LeftShift3(v.y) 需要整体左移1个bit,LeftShift3(v.z)则是2个bit,填满了总共3 * 10 = 30个bit(还有2个0bit可不管)。
实现代码如下:
inline uint32_t EncodeMorton3(const Vector3dF &v) {
Assert(v.x >= 0 && v.x <= (1 << 10));
Assert(v.y >= 0 && v.y <= (1 << 10));
Assert(v.z >= 0 && v.z <= (1 << 10));
return (LeftShift3(v.z) << 2) | (LeftShift3(v.y) << 1) | LeftShift3(v.x);
}
示意图:
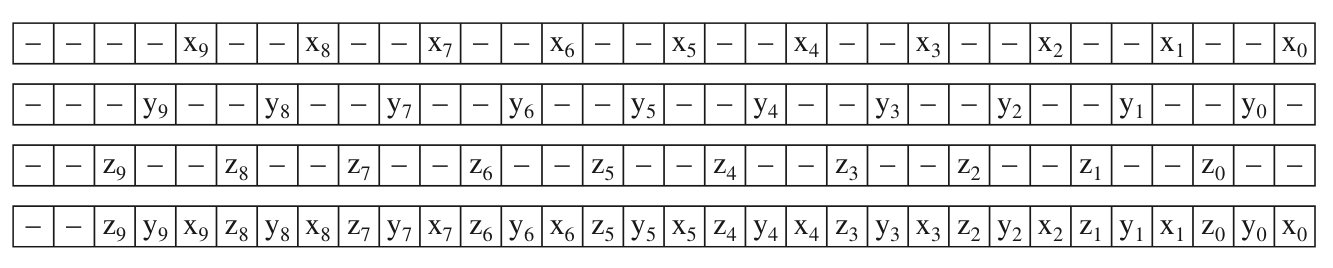
HLBVHBuild 概览
BVHBuildNode *BVHSystem::HLBVHBuild(
ComponentHandle<BVHAccel> bvhAccel,
MemoryArena &arena,
const std::vector<BVHObjInfo> &objInfo,
int *totalNodes,
std::vector<ObjectID> &orderedObjs) {
// 1. 计算所有物体中心坐标的包围盒
BBox bounds;
for (const BVHObjInfo &pi : objInfo)
bounds = Union(bounds, pi.centroid);
// 2. 并行计算每所有物体的MortonObj信息
std::vector<MortonObj> mortonObjs(objInfo.size());
ParallelFor([&](int i) {
// 莫顿码共10位
constexpr int mortonBits = 10;
constexpr int mortonScale = 1 << mortonBits;
mortonObjs[i].objIndex = objInfo[i].objNumber;
// centroidOffset是该obj中心在包围盒里的百分比坐标
Vector3dF centroidOffset = bounds.Offset(objInfo[i].centroid);
// 把百分比坐标映射到[0, 1024],然后编成莫顿码
mortonObjs[i].mortonCode = EncodeMorton3(centroidOffset * mortonScale);
}, objInfo.size(), 512);
// 3. mortonObjs数组做基数排序
RadixSort(&mortonObjs);
// 4. 按照莫顿码的高位是否一样(都属于同一个grid),对所有物体分组
// 如果物体分布很稀疏的话,就是一个物体一个treelet, nObjs为1
// (treelet可以叫做幼树,意指整个BVH树的下层部分的单个子树)
// 被mask为1的bits有12个,所以总共有2^12=4096个grid (treelet)
// 因为有3个维度,所以单维度上是2^4=16个grid
std::vector<LBVHTreelet> treeletsToBuild;
for (int start = 0, end = 1; end <= (int)mortonObjs.size(); ++end) {
uint32_t mask = 0b00111111111111000000000000000000;
if (end == (int)mortonObjs.size() ||
((mortonObjs[start].mortonCode & mask) !=
(mortonObjs[end].mortonCode & mask))) {
int nObjs = end - start;
int maxBVHNodes = 2 * nObjs;
BVHBuildNode *nodes = arena.Alloc<BVHBuildNode>(maxBVHNodes, false);
treeletsToBuild.push_back({ start, nObjs, nodes });
start = end;
}
}
// 5.开始构造BVH了
// 5.1 这段代码最关键的就是并行调用emitLBVH,和统计totalNodes
// 注意,这里构建了n个BVH子树,n=treeletsToBuild.size()
// 下一个步骤会把这n个BVH子树当成n个物体,和recursiveBuild一样自顶向下构建BVH
std::atomic<int> atomicTotal(0), orderedObjsOffset(0);
orderedObjs.resize(bvhAccel->objs.size());
ParallelFor([&](int i) {
// Generate _i_th LBVH treelet
int nodesCreated = 0;
const int firstBitIndex = 29 - 12;
LBVHTreelet &tr = treeletsToBuild[i];
tr.buildNodes = emitLBVH(bvhAccel, tr.buildNodes, objInfo, &mortonObjs[tr.startIndex],
tr.nObjs, &nodesCreated, orderedObjs,
&orderedObjsOffset, firstBitIndex);
atomicTotal += nodesCreated;
}, treeletsToBuild.size());
*totalNodes = atomicTotal;
// 5.2 把std::vector<LBVHTreelet>的buildNodes 放进 finishedTreelets
std::vector<BVHBuildNode *> finishedTreelets;
finishedTreelets.reserve(treeletsToBuild.size());
for (LBVHTreelet &treelet : treeletsToBuild)
finishedTreelets.push_back(treelet.buildNodes);
// 5.3 构造BVH的上层部分
return buildUpperSAH(arena, finishedTreelets, 0, finishedTreelets.size(),
totalNodes);
}
RadixSort
static void RadixSort(std::vector<MortonObj> *v) {
std::vector<MortonObj> tempVector(v->size());
constexpr int bitsPerPass = 6;
constexpr int nBits = 30;
Assert((nBits % bitsPerPass) == 0);
constexpr int nPasses = nBits / bitsPerPass;
for (int pass = 0; pass < nPasses; ++pass) {
// Perform one pass of radix sort, sorting _bitsPerPass_ bits
int lowBit = pass * bitsPerPass;
// Set in and out vector pointers for radix sort pass
std::vector<MortonObj> &in = (pass & 1) ? tempVector : *v;
std::vector<MortonObj> &out = (pass & 1) ? *v : tempVector;
// Count number of zero bits in array for current radix sort bit
constexpr int nBuckets = 1 << bitsPerPass;
int bucketCount[nBuckets] = { 0 };
constexpr int bitMask = (1 << bitsPerPass) - 1;
for (const MortonObj &mp : in) {
int bucket = (mp.mortonCode >> lowBit) & bitMask;
Assert(bucket >= 0 && bucket < nBuckets);
++bucketCount[bucket];
}
// Compute starting index in output array for each bucket
int outIndex[nBuckets];
outIndex[0] = 0;
for (int i = 1; i < nBuckets; ++i)
outIndex[i] = outIndex[i - 1] + bucketCount[i - 1];
// Store sorted values in output array
for (const MortonObj &mp : in) {
int bucket = (mp.mortonCode >> lowBit) & bitMask;
out[outIndex[bucket]++] = mp;
}
}
// Copy final result from _tempVector_, if needed
if (nPasses & 1) std::swap(*v, tempVector);
}
emitLBVH
emitLBVH会递归调用自己,自顶向下构建BVH树。
注意,emitLBVH依然采用自顶向下的构建流程,但是却可以多线程并行构建n(1<=n<=4096)个grid的BVH,这是第一个性能优化点;第二个性能优化点,在于emitLBVH构造BVH是线性的,即O(n)时间复杂度,这归功于前面的莫顿码排序。
BVHBuildNode *BVHSystem::emitLBVH(ComponentHandle<BVHAccel> bvhAccel,
BVHBuildNode *&buildNodes,
const std::vector<BVHObjInfo> &objInfo,
MortonObj *mortonObjs, int nObjs, int *totalNodes,
std::vector<ObjectID> &orderedObjs,
std::atomic<int> *orderedObjsOffset, int bitIndex) {
Assert(nObjs > 0);
if (bitIndex == -1 || nObjs < bvhAccel->maxObjsInNode) {
// Create and return leaf node of LBVH treelet
(*totalNodes)++;
BVHBuildNode *node = buildNodes++;
BBox bounds;
// 对orderedObjsOffset做原子操作:+=nObjs。并返回+=前的值
int firstObjOffset = orderedObjsOffset->fetch_add(nObjs);
for (int i = 0; i < nObjs; ++i) {
int objIndex = mortonObjs[i].objIndex;
orderedObjs[firstObjOffset + i] = bvhAccel->objs[objIndex];
bounds = Union(bounds, objInfo[objIndex].bounds);
}
InitLeaf(node, firstObjOffset, nObjs, bounds);
return node;
}
else {
int mask = 1 << bitIndex;
// 如果第一个物体和最后一个物体的mask bit是一样的,那么这批物体位置很集中,可直接进入下一个 mask bit
if ((mortonObjs[0].mortonCode & mask) ==
(mortonObjs[nObjs - 1].mortonCode & mask))
return emitLBVH(bvhAccel, buildNodes, objInfo, mortonObjs, nObjs,
totalNodes, orderedObjs, orderedObjsOffset,
bitIndex - 1);
// 二分查找切分位置,即mask bit发生‘突变’的物体的索引
int searchStart = 0, searchEnd = nObjs - 1;
while (searchStart + 1 != searchEnd) {
Assert(searchStart != searchEnd);
int mid = (searchStart + searchEnd) / 2;
if ((mortonObjs[searchStart].mortonCode & mask) ==
(mortonObjs[mid].mortonCode & mask))
searchStart = mid;
else {
Assert((mortonObjs[mid].mortonCode & mask) ==
(mortonObjs[searchEnd].mortonCode & mask));
searchEnd = mid;
}
}
int splitOffset = searchEnd;
Assert(splitOffset <= nObjs - 1);
Assert((mortonObjs[splitOffset - 1].mortonCode & mask) !=
(mortonObjs[splitOffset].mortonCode & mask));
// 找到切分点了,现在建立一个内部节点node,并对切分点左右两批物体递归调用emitLBVH,建立子树
(*totalNodes)++;
BVHBuildNode *node = buildNodes++; // 内部节点
// lbvh[0]和lbvh[1]分别是node的左右孩子节点
BVHBuildNode *lbvh[2] = {
emitLBVH(bvhAccel, buildNodes, objInfo, mortonObjs, splitOffset,
totalNodes, orderedObjs, orderedObjsOffset,
bitIndex - 1),
emitLBVH(bvhAccel, buildNodes, objInfo, &mortonObjs[splitOffset], nObjs - splitOffset,
totalNodes, orderedObjs, orderedObjsOffset,
bitIndex - 1) };
// 这个mask bit对应的是哪条坐标轴
Axis axis = static_cast<Axis>(bitIndex % 3);
InitInterior(node, axis, lbvh[0], lbvh[1]);
return node;
}
}
buildUpperSAH
对所有treelet,自顶向下构建BVH的上层部分,用了递归。
第一次调用buildUpperSAH创建的是根节点,包含所有treelet;
如果nNodes为1,那么已经到达某个treelet,终止递归;
如果nNodes > 1,创建内部节点,并调用2次buildUpperSAH,创建该内部节点的左右子树。
BVHBuildNode *BVHSystem::buildUpperSAH(MemoryArena &arena, std::vector<BVHBuildNode *> &treeletRoots,
int start, int end,
int *totalNodes) {
Assert(start < end);
int nNodes = end - start;
if (nNodes == 1) return treeletRoots[start]; // 已经到底了,终止递归
(*totalNodes)++;
BVHBuildNode *node = arena.Alloc<BVHBuildNode>();
// Compute bounds of all nodes under this HLBVH node
BBox bounds;
for (int i = start; i < end; ++i)
bounds = Union(bounds, treeletRoots[i]->bounds);
// Compute bound of HLBVH node centroids, choose split dimension _dim_
BBox centroidBounds;
for (int i = start; i < end; ++i) {
Vector3dF centroid =
(treeletRoots[i]->bounds.pMin + treeletRoots[i]->bounds.pMax) *
0.5f;
centroidBounds = Union(centroidBounds, centroid);
}
Axis dim = centroidBounds.MaximumExtent();
// FIXME: if this hits, what do we need to do?
// Make sure the SAH split below does something... ?
Assert(centroidBounds.pMax[dim] != centroidBounds.pMin[dim]);
// 计算buckets, 可参考recursiveBuild
constexpr int nBuckets = 12;
BucketInfo buckets[nBuckets];
for (int i = start; i < end; ++i) {
float centroid = (treeletRoots[i]->bounds.pMin[dim] +
treeletRoots[i]->bounds.pMax[dim]) *
0.5f;
int b =
nBuckets * ((centroid - centroidBounds.pMin[dim]) /
(centroidBounds.pMax[dim] - centroidBounds.pMin[dim]));
if (b == nBuckets) b = nBuckets - 1;
Assert(b >= 0 && b < nBuckets);
buckets[b].count++;
buckets[b].bounds = Union(buckets[b].bounds, treeletRoots[i]->bounds);
}
float cost[nBuckets - 1];
computeCosts(bounds, cost, buckets, nBuckets, .125f);
float minCost;
int minCostSplitBucket;
findMinCost(cost, nBuckets, &minCost, &minCostSplitBucket);
// 每个treelet拿自己的bucket值和minCostSplitBucket比较大小,切分成2部分
BVHBuildNode **pmid = std::partition(
&treeletRoots[start], &treeletRoots[end - 1] + 1,
[=](const BVHBuildNode *node) {
float centroid =
(node->bounds.pMin[dim] + node->bounds.pMax[dim]) * 0.5f;
int b = nBuckets *
((centroid - centroidBounds.pMin[dim]) /
(centroidBounds.pMax[dim] - centroidBounds.pMin[dim]));
if (b == nBuckets) b = nBuckets - 1;
Assert(b >= 0 && b < nBuckets);
return b <= minCostSplitBucket;
});
int mid = pmid - &treeletRoots[0];
Assert(mid > start && mid < end);
InitInterior(node,
dim, buildUpperSAH(arena, treeletRoots, start, mid, totalNodes),
buildUpperSAH(arena, treeletRoots, mid, end, totalNodes));
return node;
}
总结
HLBVHBuild的特点:
把整个BVH树的构建,拆成上层、下层两部分工作:
下层:并行构建treelet(幼树)
上层:把构建好的所有treelet作为叶子节点,进而构造BVH上层部分
和recursiveBuild,依然还是用自顶向下的构造流程(上层、下层都是)
HLBVHBuild的上层部分计算和recursiveBuild基本是一样的,并没有什么改进,一样用了SAH算法
HLBVHBuild的下层部分计算才是性能关键之处:
关键点1:对所有物体进行了莫顿编码,莫顿编码后用了自定义的高效基数排序,然后就可以快速把所有物体根据空间位置分组,生成treelet
关键点2: 用了多线程从而并行构建treelet的BVH结构
关键点3:每个treelet还可以利用排好序的莫顿码信息,线性(O(n)复杂度)构建treelet的BVH结构
总之,HLBVHBuild实际上是在recursiveBuild的基础上,做了改进的版本,因为HLBVHBuild的上层部分就相当于recursiveBuild。
另外,HLBVHBuild也可以认为是自底向上的算法,因为是先遍历了所有物体算莫顿码并构建各个treelet。
写作不易,您的支持是我写作的动力!

